
【题目】已知抛物线C1:y=x2+2x﹣3与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线C2:y=ax2+bx+c经过点B,与x轴的另一个交点为E(﹣4,0),与y轴交于点D(0,2).
(1)求抛物线C2的解析式;
(2)设点P为线段AB上一动点(点P不与点A,B重合),过点P作x轴的垂线交抛物线C1于点M,交抛物线C2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.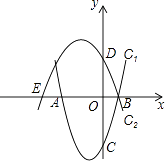
【答案】
(1)
解:在y=x2+2x﹣3中,令y=0可得0=x2+2x﹣3,解得x=﹣3或x=1,令x=0可得y=﹣3,
∴A(﹣3,0),B(1,0),C(0,﹣3),
设抛物线C2的解析式为y=ax2+bx+c,
把B、D、E三点坐标代入可得 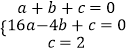 ,解得
,解得 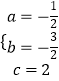 ,
,
∴抛物线C2的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)
解:设P(x,0)(﹣3<x<1),则M(x,x2+2x﹣3),N(x,﹣ ![]() x2﹣
x2﹣ ![]() x+2),
x+2),
①∵点P为线段AB上一动点,
∴MN=﹣ ![]() x2﹣
x2﹣ ![]() x+2﹣(x2+2x﹣3)=﹣
x+2﹣(x2+2x﹣3)=﹣ ![]() x2﹣
x2﹣ ![]() x+5,
x+5,
∴S四边形AMBN= ![]() ABMN=
ABMN= ![]() ×4(﹣
×4(﹣ ![]() x2﹣
x2﹣ ![]() x+5)=﹣3x2﹣7x+10=﹣3(x+
x+5)=﹣3x2﹣7x+10=﹣3(x+ ![]() )2+
)2+ ![]() ,
,
∵﹣3<0,
∴当x=﹣ ![]() 时,S四边形AMBN有最大值,
时,S四边形AMBN有最大值,
此时P点坐标为(﹣ ![]() ,0);
,0);
②分CM和DN平行和不平行两种情况,
当CM与DN不平行时,如图1,作MF⊥CD于F,NG⊥CD于G,

在Rt△MFC和Rt△NGD中
![]()
∴Rt△MFC≌Rt△NGD(HL),
∴FC=GD,
∴PM﹣PN=FO﹣OG=OC﹣OD=3﹣2=1,
∴﹣x2﹣2x+3﹣(﹣ ![]() x2﹣
x2﹣ ![]() x+2)=1,解得x=﹣1或x=0(舍去),
x+2)=1,解得x=﹣1或x=0(舍去),
∴P(﹣1,0);
当CM∥DN时,如图2,
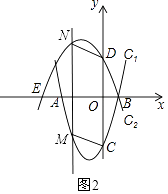
则四边形MNDC为平行四边形,
∴MN=CD=2+3=5,
∴﹣ ![]() x2﹣
x2﹣ ![]() x+5=5,解得x=0(舍去)或x=﹣
x+5=5,解得x=0(舍去)或x=﹣ ![]() ,
,
∴P(﹣ ![]() ,0);
,0);
综上可知P点坐标为(﹣1,0)或(﹣ ![]() ,0)
,0)
【解析】(1)可先求得A、B、C的坐标,利用待定系数法可求得抛物线C2的解析式;(2)可设P(x,0),①则可表示出M、N的坐标,可表示出MN的长,从而可用x表示出四边形AMBN的面积,利用二次函数的性质可求得当其取最大值时x的值,可求得P点坐标;②分CM和DN平行和不平行两种情况,分别构造全等三角形可得到关于x的方程,从而可求得P点坐标.
【考点精析】本题主要考查了二次函数的性质和二次函数的最值的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴的正半轴相交,顶点在第四象限,对称轴为x=1,下列结论:①b<0;②a+b<0;③ ![]() <﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( )
<﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( ) 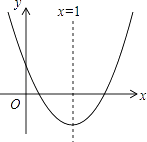
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
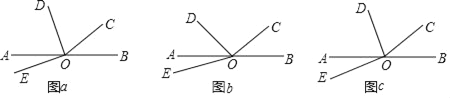
【题目】如图,O为直线AB上一点,∠BOC=α.
(1)若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;
(2)若∠AOD=![]() ∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
(3)若∠AOD=![]() ∠AOC,∠DOE=
∠AOC,∠DOE=![]() (n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).
(n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图数轴上两点A、B所别应的分别为﹣3、1,点P在数轴上从点A出发以每秒钟2个单位的长度的速度向右运动,点Q在数轴上从点B出发以每秒钟1个单位长度的速度向左运动,设点P的运动时间为t秒.
(1)直接写出线段AB的中点所对应的数及t秒后点P所对应的数.
(2)若点P和点Q同时出发,求点P和点Q相遇时的位置所对应的数;
(3)若点P比点Q迟1秒钟出发,问点P出发几秒后,点P和点Q刚好相距1个单位长度.并问此时数轴上是否存在一个点C,使其到点A、点P和点Q这三点的距离和最小?若存在,直接写出点C所对应的数;若不存在,试说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
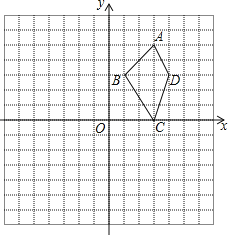
【题目】四边形ABCD在平面直角坐标系的位置如图所示,将四边形ABCD先向下平移2个单位,再向左平移3个单位得到四边形A1B1C1D1,解答下列各题:
(1)请在图中画出四边形A1B1C1D1;
(2)请写出四边形A1B1C1D1的顶点B1、D1坐标;
(3)请求出四边形A1B1C1D1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
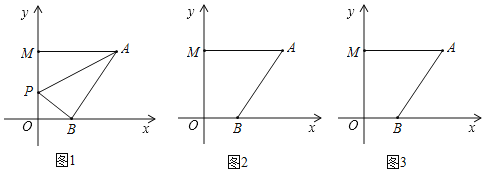
【题目】在平面直角坐标系中,A(6,a),B(b,0),M(0,c),P点为y轴上一动点,且(b﹣2)2+|a﹣6|+![]() =0.
=0.
(1)求点B、M的坐标;
(2)当P点在线段OM上运动时,试问是否存在一个点P使S△PAB=13,若存在,请求出P点的坐标与AB的长度;若不存在,请说明理由.
(3)不论P点运动到直线OM上的任何位置(不包括点O、M),∠PAM、∠APB、∠PBO三者之间是否都存在某种固定的数量关系,如果有,请利用所学知识找出并证明;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1 , m)、B(x1+n,m)两点,则m、n的关系为( )
A.m= ![]() n
n
B.m= ![]() n
n
C.m= ![]()
![]()
D.m= ![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com