Question

如图，AD∥BC，EF∥AD， CE平分∠BCF，∠DAC＝120°，∠ACF＝20°，求∠FEC的度数．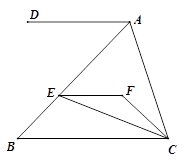

Answer 1

20°

解析试题分析：根据平行线的性质可得∠DAC+∠ACB=180°，即可求得∠ACB的度数，再由∠ACF＝20°可得∠BCF的度数，再根据角平分线的性质可得∠BCE的度数，由EF∥AD根据平行公理的推论可得EF∥BC，最后根据平行线的性质求解即可.
∵AD∥BC  （已知）    
∴∠DAC+∠ACB=180° （两直线平行，同旁内角互补）
∵∠DAC＝120° （已知）
∴∠ACB＝180°－120°=60°
∵∠ACF＝20° （已知） 
∴∠BCF＝60°－20°=40° 
∵CE平分∠BCF （已知）
∴∠BCE=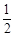∠BCF=20°  (角平分线的定义)
∵EF∥AD   （已知）
∴EF∥BC     （平行公理的推论）
∴∠FEC=∠BCE=20° （两直线平行，内错角相等）
考点：平行线的判定和性质，角平分线的性质
点评：平行线的判定和性质是初中数学的重点，贯穿于整个初中数学的学习，是中考常见题，一般难度不大，需熟练掌握.