
 .
. ∴抛物线解析式为:y=-
∴抛物线解析式为:y=- (x-6)2+6,即y=-
(x-6)2+6,即y=- x2+2x;
x2+2x; m2+2m),D(m,-
m2+2m),D(m,- m2+2m).
m2+2m). m2+2m)+(12-2m)+(-
m2+2m)+(12-2m)+(- m2+2m)
m2+2m) m2+2m+12
m2+2m+12 (m-3)2+15.
(m-3)2+15.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
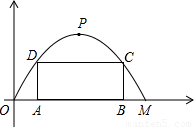
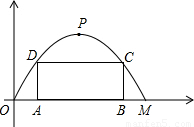
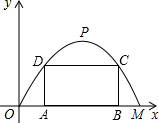 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
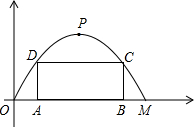 如图,某公路隧道横截面为抛物线,其最大高度6米,底部宽度OM为12米,现以O点为原点,OM所在的直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度6米,底部宽度OM为12米,现以O点为原点,OM所在的直线为x轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(20):20.5 二次函数的一些应用(解析版) 题型:解答题
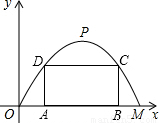 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源:2012届吉林省初三上学期第二次月考数学试卷 题型:解答题
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.
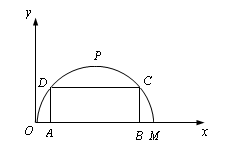
1.直接写出点M及抛物线顶点P的坐标;
2.求这条抛物线的解析式;
3.若要搭建一个矩形“支撑架”AD- DC- CB,
使C、D点在抛物线上,A、B点在地面OM上,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com