
”¾ĢāÄæ”æŌŚŃ§Ļ°Čż½ĒŠĪÖŠĪ»ĻߵĊŌÖŹŹ±£¬Š”ĮĮ¶ŌæĪ±¾øų³öµÄ½ā¾ö°ģ·Ø½ųŠŠĮĖČĻÕęĖ¼æ¼£ŗ 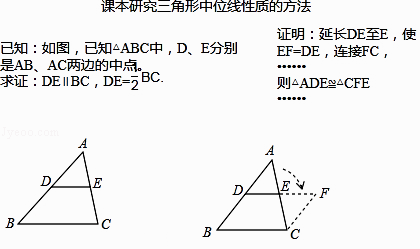 ĒėÄćĄūÓĆŠ”ĮĮµÄ·¢ĻÖ½ā¾öĻĀĮŠĪŹĢā£ŗ
ĒėÄćĄūÓĆŠ”ĮĮµÄ·¢ĻÖ½ā¾öĻĀĮŠĪŹĢā£ŗ
£Ø1£©ČēĶ¼1£¬ADŹĒ”÷ABCµÄÖŠĻߣ¬BE½»ACÓŚE£¬½»ADÓŚE£¬ĒŅAE=EF£¬ĒóÖ¤£ŗAC=BF£® ĒėÄć°ļÖśŠ”ĮĮŠ“³öøØÖśĻß×÷·Ø²¢Ķź³ÉĀŪÖ¤¹ż³Ģ£ŗ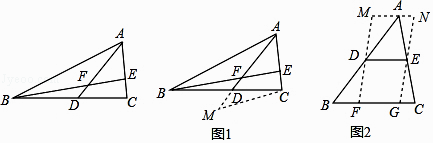
£Ø2£©½ā¾öĪŹĢā£ŗČēĶ¼2£¬ŌŚ”÷ABCÖŠ£¬”ĻB=45”ć£¬AB=10£¬BC=8£¬DEŹĒ”÷ABCµÄÖŠĪ»Ļߣ¬¹żµćD”¢E×÷DF”ĪEG£¬·Ö±š½»BCÓŚF”¢G£¬¹żµćA×÷MN”ĪBC£¬·Ö±šÓėFE”¢GEµÄŃÓ³¤Ļß½»ÓŚM”¢N£¬ŌņĖıߊĪMFGNÖܳ¤µÄ×īŠ”ÖµŹĒ £®
”¾“š°ø”æ
£Ø1£©Ö¤Ć÷£ŗČēĶ¼1£¬ŃÓ³¤ADÖĮµćM£¬Ź¹MD=FD£¬Į¬½ÓMC£¬
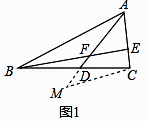
ŌŚ”÷BDFŗĶ”÷CDMÖŠ£¬ 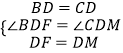 £¬
£¬
”ą”÷BDF”Õ”÷CDM£ØSAS£©£®
”ąMC=BF£¬”ĻM=”ĻBFM£®
”ßEA=EF£¬
”ą”ĻEAF=”ĻEFA£¬
”ß”ĻAFE=”ĻBFM£¬
”ą”ĻM=”ĻMAC£¬
”ąAC=MC£¬
”ąBF=AC
£Ø2£©10 ![]() +8
+8
”¾½āĪö”æ£Ø2£©½ā£ŗČēĶ¼2£¬ 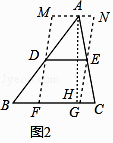
”ßMN”ĪBC£¬FM”ĪGN£¬
”ąĖıߊĪMFGNŹĒĘ½ŠŠĖıߊĪ£¬
”ąMF=NG£¬MN=FG£¬
”ßDEŹĒ”÷ABCµÄÖŠĪ»Ļߣ¬
”ąDE= ![]() BC=4£¬DE”ĪBC£¬
BC=4£¬DE”ĪBC£¬
”ąMN=FG= ![]() BC=4£¬
BC=4£¬
”ąĖıߊĪMFGNÖܳ¤=2£ØMF+FG£©=2MF+8£¬
”ąMF”ĶBCŹ±£¬MF×ī¶Ģ£¬
¼“£ŗĖıߊĪMFGNµÄÖܳ¤×īŠ”£¬
¹żµćA×÷AH”ĶBCÓŚH£¬
”ąFM=AH
ŌŚRt”÷ABHÖŠ£¬”ĻB=45”ć£¬AB=10£¬
”ąAH= ![]() =5
=5 ![]() £¬
£¬
”ąĖıߊĪMFGNµÄÖܳ¤×īŠ”ĪŖ2MF+8=10 ![]() +8£®
+8£®
ĖłŅŌ“š°øŹĒ£ŗ10 ![]() +8£®
+8£®
”¾æ¼µć¾«Īö”æøł¾ŻĢāÄæµÄŅŃÖŖĢõ¼ž£¬ĄūÓĆČż½ĒŠĪÖŠĪ»Ļß¶ØĄķµÄĻą¹ŲÖŖŹ¶æÉŅŌµĆµ½ĪŹĢāµÄ“š°ø£¬ŠčŅŖÕĘĪÕĮ¬½ÓČż½ĒŠĪĮ½±ßÖŠµćµÄĻ߶Ī½Š×öČż½ĒŠĪµÄÖŠĪ»Ļߣ»Čż½ĒŠĪÖŠĪ»Ļß¶ØĄķ£ŗČż½ĒŠĪµÄÖŠĪ»ĻßĘ½ŠŠÓŚČż½ĒŠĪµÄµŚČż±ß£¬ĒŅµČÓŚµŚČż±ßµÄŅ»°ė£®


 ĆūŠ£Į·æ¼¾ķĘŚÄ©³å“Ģ¾ķĻµĮŠ“š°ø
ĆūŠ£Į·æ¼¾ķĘŚÄ©³å“Ģ¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=ax2+bx+1ÓėÖ±Ļßy=©ax+cĻą½»ÓŚ×ų±źÖįÉĻµćA£Ø©3£¬0£©£¬C£Ø0£¬1£©Į½µć£®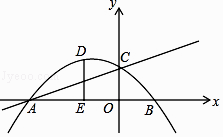
£Ø1£©Ö±Ļߵıķ“ļŹ½ĪŖ£»Å×ĪļĻߵıķ“ļŹ½ĪŖ £®
£Ø2£©DĪŖÅ×ĪļĻßŌŚµŚ¶žĻóĻŽ²æ·ÖÉĻµÄŅ»µć£¬×÷DE“¹Ö±xÖįÓŚµćE£¬½»Ö±ĻßACÓŚµćF£¬ĒóĻ߶ĪDF³¤¶ČµÄ×ī“óÖµ£¬²¢Ēó“ĖŹ±µćDµÄ×ų±ź£»
£Ø3£©PĪŖÅ×ĪļĻßÉĻŅ»¶Æµć£¬ĒŅPŌŚµŚĖÄĻóĻŽÄŚ£¬¹żµćP×÷PN“¹Ö±xÖįÓŚµćN£¬Ź¹µĆŅŌP”¢A”¢NĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ACOĻąĖĘ£¬ĒėÖ±½ÓŠ“³öµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£¬ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Õż±ČĄżŗÆŹży= ![]() xµÄĶ¼Ļń¾¹żµćA£¬µćAµÄׯ×ų±źĪŖ6£¬·“±ČĄżŗÆŹży=
xµÄĶ¼Ļń¾¹żµćA£¬µćAµÄׯ×ų±źĪŖ6£¬·“±ČĄżŗÆŹży= ![]() µÄĶ¼ĻńŅ²¾¹żµćA£¬µŚŅ»ĻóĻŽÄŚµÄµćBŌŚÕāøö·“±ČĄżŗÆŹżµÄĶ¼ĻńÉĻ£¬¹żµćB×÷BC”ĪxÖį£¬½»yÖįÓŚµćC£¬ĒŅAC=AB£¬Ēó£ŗ
µÄĶ¼ĻńŅ²¾¹żµćA£¬µŚŅ»ĻóĻŽÄŚµÄµćBŌŚÕāøö·“±ČĄżŗÆŹżµÄĶ¼ĻńÉĻ£¬¹żµćB×÷BC”ĪxÖį£¬½»yÖįÓŚµćC£¬ĒŅAC=AB£¬Ēó£ŗ 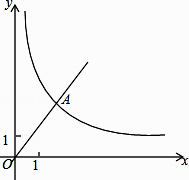
£Ø1£©Õāøö·“±ČĄżŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©Ö±ĻßAB£ØŅ»“ĪŗÆŹż£©µÄ±ķ“ļŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓĆ”°*”±¶ØŅåŅ»ÖÖŠĀŌĖĖć£ŗ¶ŌÓŚČĪŅāÓŠĄķŹżaŗĶb£¬¹ę¶Øa*b=ab2+2ab+a£®
Čē£ŗ1*3=1”Į32+2”Į1”Į3+1=16
£Ø1£©Ēó2*£Ø©2£©µÄÖµ£»
£Ø2£©Čō2*x=m,![]() £ØĘäÖŠxĪŖÓŠĄķŹż£©£¬ŹŌ±Č½Ļm£¬nµÄ“󊔣»
£ØĘäÖŠxĪŖÓŠĄķŹż£©£¬ŹŌ±Č½Ļm£¬nµÄ“󊔣»
£Ø3£©Čō[![]() ]
]![]() =a+4£¬ĒóaµÄÖµ£®
=a+4£¬ĒóaµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬AB£½10£¬AC£½2![]() £¬BC±ßÉĻµÄøßAD£½6£¬ŌņĮķŅ»±ßBCµČÓŚ_______£®
£¬BC±ßÉĻµÄøßAD£½6£¬ŌņĮķŅ»±ßBCµČÓŚ_______£®
”¾“š°ø”æ10»ņ6
”¾½āĪö”æŹŌĢā½āĪö£ŗøł¾ŻĢāŅā»³öĶ¼ŠĪ£¬ČēĶ¼ĖłŹ¾£¬

ČēĶ¼1ĖłŹ¾£¬AB=10£¬AC=2![]() £¬AD=6£¬
£¬AD=6£¬
ŌŚRt”÷ABDŗĶRt”÷ACDÖŠ£¬
øł¾Ż¹“¹É¶ØĄķµĆ£ŗBD=![]() =8£¬CD=
=8£¬CD=![]() =2£¬
=2£¬
“ĖŹ±BC=BD+CD=8+2=10£»
ČēĶ¼2ĖłŹ¾£¬AB=10£¬AC=2![]() £¬AD=6£¬
£¬AD=6£¬
ŌŚRt”÷ABDŗĶRt”÷ACDÖŠ£¬
øł¾Ż¹“¹É¶ØĄķµĆ£ŗBD=![]() =8£¬CD=
=8£¬CD=![]() =2£¬
=2£¬
“ĖŹ±BC=BD-CD=8-2=6£¬
ŌņBCµÄ³¤ĪŖ6»ņ10£®
”¾ĢāŠĶ”æĢīæÕĢā
”¾½įŹų”æ
12
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖŅ»“ĪŗÆŹży=2x+1µÄĶ¼Ļó¾¹żP1£Øx1£¬y1£©”¢P2£Øx2£¬y2£©Į½µć£¬Čōx1£¼x2£¬Ōņy1 ______ y2£®£ØĢī”°£¾”±”°£¼”±»ņ”°=”±£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚČēĶ¼ĖłŹ¾µÄ5”Į5ĶųøńÖŠ£¬Š”·½øńµÄ±ß³¤ĪŖ1.
(1)Ķ¼ÖŠøńµćÕż·½ŠĪABCDµÄĆ껿ĪŖ________£»
(2)ČōĮ¬½ÓAC£¬ŌņŅŌACĪŖ±ßµÄÕż·½ŠĪµÄĆ껿ĪŖ________£»
(3)ŌŚĖłøųĶųøńÖŠ»Ņ»øöøńµćÕż·½ŠĪ£¬Ź¹Ęäø÷±ß¶¼²»ŌŚøńĻßÉĻĒŅĆ껿×ī“ó£¬ÄćĖł»µÄÕż·½ŠĪĆ껿ĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČż½ĒŠĪABCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬ĘäÖŠ”ĻA=90”ć£¬BC³¤ĪŖ6.
(1)½ØĮ¢ŹŹµ±µÄÖ±½Ē×ų±źĻµ£¬²¢Š“³öø÷øö¶„µćµÄ×ų±ź.
(2)½«(1)ÖŠø÷¶„µćµÄŗį×ų±ź²»±ä£¬½«×Ż×ų±ź¶¼³Ė-1£¬ÓėŌĶ¼°øĻą±Č£¬ĖłµĆµÄĶ¼°øÓŠŹ²Ć“±ä»Æ£æ
(3)½«(1)ÖŠø÷¶„µćµÄŗį×ų±ź¶¼³Ė-2£¬×Ż×ų±ź±£³Ö²»±ä£¬ÓėŌĶ¼°øĻą±Č£¬ĖłµĆµÄĶ¼°øÓŠŹ²Ć“±ä»Æ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪABCDŗĶÕż·½ŠĪA1B1C1D1µÄ¶Ō½ĒĻß(Õż·½ŠĪĻą¶Ō¶„µćÖ®¼äĖłĮ¬µÄĻ߶Ī)BD£¬B1D1¶¼ŌŚxÖįÉĻ£¬O£¬O1·Ö±šĪŖÕż·½ŠĪABCDŗĶÕż·½ŠĪA1B1C1D1µÄÖŠŠÄ(Õż·½ŠĪ¶Ō½ĒĻߵĽ»µć³ĘĪŖÕż·½ŠĪµÄÖŠŠÄ)£¬OĪŖĘ½ĆęÖ±½Ē×ų±źĻµµÄŌµć£®OD£½3£¬O1D1£½2.
(1)Čē¹ūO1ŌŚxÖįÉĻĘ½ŅĘŹ±£¬Õż·½ŠĪA1B1C1D1Ņ²ĖęÖ®Ę½ŅĘ£¬ĘäŠĪד”¢“óŠ”ƻӊøı䣬µ±ÖŠŠÄO1ŌŚxÖįÉĻĘ½Ņʵ½Į½øöÕż·½ŠĪÖ»ÓŠŅ»øö¹«¹²µćŹ±£¬Ēó“ĖŹ±Õż·½ŠĪA1B1C1D1ø÷¶„µćµÄ×ų±ź£»
(2)Čē¹ūOŌŚxÖįÉĻĘ½ŅĘŹ±£¬Õż·½ŠĪABCDŅ²ĖęÖ®Ę½ŅĘ£¬ĘäŠĪד”¢“óŠ”ƻӊøı䣬µ±ÖŠŠÄOŌŚxÖįÉĻĘ½Ņʵ½Į½øöÕż·½ŠĪ¹«¹²²æ·ÖµÄĆ껿ĪŖ2øöĘ½·½µ„Ī»Ź±£¬Ēó“ĖŹ±Õż·½ŠĪABCDø÷¶„µćµÄ×ų±ź£®
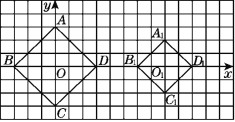
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬OB£¬AB±ķŹ¾¼×”¢ŅŅĮ½ĆūĶ¬Ń§ŌĖ¶ÆµÄŅ»“ĪŗÆŹżĶ¼Ļó£¬Ķ¼ÖŠsŗĶt·Ö±š±ķŹ¾ŌĖ¶ÆĀ·³ĢŗĶŹ±¼ä£¬ŅŃÖŖ¼×µÄĖŁ¶Č±ČŅŅæģ£¬ĻĀĮŠĖµ·Ø£ŗ¢ŁÉäĻßAB±ķŹ¾¼×µÄĀ·³ĢÓėŹ±¼äµÄŗÆŹż¹ŲĻµ£»¢Ś¼×µÄĖŁ¶Č±ČŅŅæģ1.5 m/s£»¢ŪŅŅŌŚ¼×Ē°Ćę12 m“¦ĘšÅÜ£»¢Ü 8 sŗ󣬼׳¬¹żĮĖŅŅ£®ĘäÖŠÕżČ·µÄĖµ·ØŹĒ(”” ””)
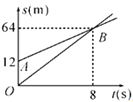
A. ¢Ł¢Ś B. ¢Ś¢Ū¢Ü C. ¢Ś¢Ū D. ¢Ł¢Ū¢Ü
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com