
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣![]() x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2).
x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2).
(1)求抛物线的表达式,并用配方法求出顶点D的坐标;
(2)若点E是点C关于抛物线对称轴的对称点,求tan∠CEB的值.

【答案】(1)y=﹣![]() x2﹣
x2﹣![]() +2,顶点D的坐标为(﹣1,
+2,顶点D的坐标为(﹣1,![]() );(2)tan∠CEB的值是
);(2)tan∠CEB的值是![]() .
.
【解析】
(1)∵抛物线y=﹣![]() x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2),
x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2),
∴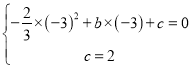 ,
,
得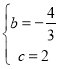 ,
,
∴y=﹣![]() x2﹣
x2﹣![]() x+2=
x+2=![]() ,
,
∴抛物线顶点D的坐标为(﹣1,![]() ),
),
即该抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+2,顶点D的坐标为(﹣1,
x+2,顶点D的坐标为(﹣1,![]() );
);
(2)∵y=![]() ,
,
∴该抛物线的对称轴为直线x=﹣1,
∵点E是点C关于抛物线对称轴的对称点,点C(0,2),
∴点E的坐标为(﹣2,2),
当y=0时,0=![]() ,得x1=﹣3,x2=1,
,得x1=﹣3,x2=1,
∴点B的坐标为(1,0),
设直线BE的函数解析式为y=kx+n,
![]() ,得
,得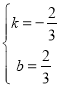 ,
,
∴直线BE的函数解析式为y=﹣![]() +
+![]() ,
,
当x=0时,y=![]() ,
,
设直线BE与y轴交于点F,则点F的坐标为(0,![]() ),
),
∴OF=![]() ,
,
∵点C(0,2),点E(﹣2,2),
∴OC=2,CE=2,
∴CF=2﹣![]() =
=![]() ,
,
∴tan∠CEF= ,
,
即tan∠CEB的值是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小明同学为筹备缤纷节财商体验活动,准备在商店购入小商品A和B.已知A和B的单价和为25元,小明计划购入A的数量比B的数量多3件,但一共不超过28件.现商店将A的单价提高20%,B打8折出售,小明决定将A、B的原定数量对调,这样实际花费比原计划少6元.已知调整前后的价格和数量均为整数,求小明原计划购买费用为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=5,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(1)线段OA1的长是 ,∠AOB1的度数是 ;
(2)连接AA1,求证:四边形OAA1B1是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
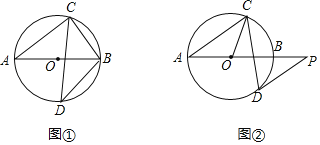
(1)如图①,若D为弧AB的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
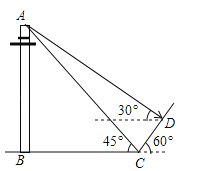
【题目】黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.
(结果精确到1m,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
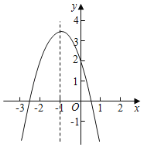
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=﹣1,有以下结论:①abc<0;②2a﹣b=0;③4ac﹣b2<8a;④3a+c<0;⑤a﹣b<m(am+b),其中正确的结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图象与性质,探究过程如下,请补充完整.
的图象与性质,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ,
,![]() ;
;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;

(3)观察函数图象:
①当方程![]() 有且仅有两个不相等的实数根,根据函数图象直接写出
有且仅有两个不相等的实数根,根据函数图象直接写出![]() 的取值范围为 ;
的取值范围为 ;
②在该平面直角坐标系中画出直线![]() 的图象,根据图象直接写出该直线与函数
的图象,根据图象直接写出该直线与函数![]()
![]() 的交点横坐标为: (结果保留一位小数).
的交点横坐标为: (结果保留一位小数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com