

分析 (1)如图一中,连接DE.由△BDC≌△BDE,推出CD=DE,∠DEB=∠DCB=90°,再证明∠CDG=∠CGD,推出CG=CD=DE=1,推出AD=$\sqrt{2}$,AC=$\sqrt{2}$+1,即可推出AB=$\sqrt{2}$AC=2+$\sqrt{2}$;
(2)如图二中,作AM⊥CE于M.首先证明△AMH是等腰直角三角形,推出AM=MH,再证明△ACM≌△CBH,推出BH=CM,CH=AM=HM,即可证明BH=2AM=$\sqrt{2}$AH;
解答 (1)解:如图一中,连接DE.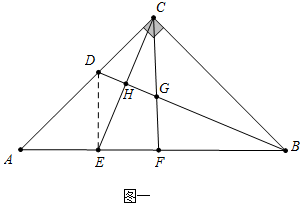
∵CE⊥BD,
∴∠BHC=∠BHE=90°,∵BH=BH,∠HBC=∠HBE,
∴△BHC≌△BHE,
∴BE=BC,∵∠DBC=∠DBE,BD=BD,
∴△BDC≌△BDE,
∴CD=DE,∠DEB=∠DCB=90°,
∵CA=CB,∠ACB=90°,CF⊥⊥AB,
∴∠A=∠BCF=45°,
∵∠CDB=∠A+∠ABD,∠CGD=∠BCG+∠CBD,
∴∠CDG=∠CGD,
∴CG=CD=DE=1,
∴AD=$\sqrt{2}$,AC=$\sqrt{2}$+1,
AB═$\sqrt{2}$AC=2+$\sqrt{2}$.
(2)证明:如图二中,作AM⊥CE于M.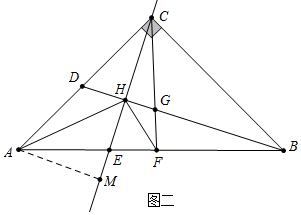
∵∠EFC=∠EHB=90°,∠BEH=∠CEF,
∴△BHE∽△CFE,
∴$\frac{EH}{EF}$=$\frac{EB}{CE}$,
∴$\frac{EH}{EB}$=$\frac{EF}{EC}$,
∴△EHF∽△EBC,
∴∠EHF=∠EBC=45°,
∵∠AHF=90°,
∴∠AHM=45°,
∵∠AMH=90°,
∴△AMH是等腰直角三角形,
∴AM=MH,
∵AC=BC,∠ACM=∠CBH,∠AMC=∠BHC=90°,
∴△ACM≌△CBH,
∴BH=CM,CH=AM=HM,
∴BH=2AM=$\sqrt{2}$AH.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 两条不相交的直线叫做平行线 | |
| B. | 一条直线的平行线有且只有一条 | |
| C. | 若直线a∥b,a∥c,则b∥c | |
| D. | 若两条线段不相交,则它们互相平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com