
分析 设甲地到乙地地行驶过程中平路、上坡、下坡各是x千米、y千米、z千米.根据路程÷速度=时间列出方程组解答即可.
解答 解:设甲地到乙地地行驶过程中平路、上坡、下坡各是x千米、y千米、z千米.则
$\left\{\begin{array}{l}{\frac{x}{30}+\frac{y}{20}+\frac{z}{40}=\frac{5}{2}}\\{\frac{x}{30}+\frac{y}{40}+\frac{z}{20}=\frac{23}{10}}\\{x+y+z=70}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=54}\\{y=12}\\{z=4}\end{array}\right.$
答:甲地到乙地地行驶过程中平路、上坡、下坡各是54千米,12千米,4千米.
点评 本题考查了三元一次方程组的应用.本题还需注意去时的上坡路回时是下坡路,去时的下坡路是回时的上坡路,平路不变.


科目:初中数学 来源: 题型:填空题
| x | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | -14 | -7 | -2 | 2 | m | n | -7 | -14 | -23 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=6,n=1 | B. | m=5,n=1 | C. | m=5,n=0 | D. | m=6,n=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
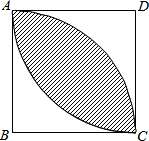 如图,在边长为a的正方形ABCD中,分别以B,D分圆心,以a为半径在正方形内部画弧,形成了叶子形图案(阴影部分),则这个叶片形图案的周长为πa.
如图,在边长为a的正方形ABCD中,分别以B,D分圆心,以a为半径在正方形内部画弧,形成了叶子形图案(阴影部分),则这个叶片形图案的周长为πa.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
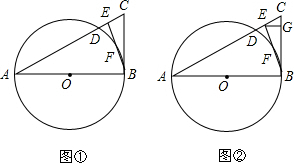
 如图,AB是⊙O的直径,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
如图,AB是⊙O的直径,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com