
【题目】已知甲、乙两地相距160km,![]() 、
、![]() 两车分别从甲、乙两地同时出发,
两车分别从甲、乙两地同时出发,![]() 车速度为85km/h,
车速度为85km/h,![]() 车速度为65km/h.
车速度为65km/h.
(1)![]() 、
、![]() 两车同时同向而行,
两车同时同向而行,![]() 车在后,经过几小时
车在后,经过几小时![]() 车追上
车追上![]() 车?
车?
(2)![]() 、
、![]() 两车同时相向而行,经过几小时两车相距20km?
两车同时相向而行,经过几小时两车相距20km?
【答案】(1)经过8小时A车追上B车;(2)经过![]() 或1.2小时两车相距20千米
或1.2小时两车相距20千米
【解析】
(1)设经过x小时A车追上B车,根据A行驶的路程比B多160千米列出方程并解答;
(2)设经过a小时两车相距20千米.分两种情况进行讨论:①相遇前两车相距20千米;②遇后两车相距20千米.
解:(1)设经过x小时A车追上B车,根据题意得:
85x-65x=160,
解之得x=8,
答:经过8小时A车追上B车;
(2)设经过a小时两车相距20千米,分两种情况:
①相遇前两车相距20千米,列方程为:
85a+65a+20=160,
解之得a=![]() ;
;
②相遇后两车相距20千米,列方程为:
85a+65a-20=160 ,
解之得a=1.2 ,
答:经过![]() 或1.2小时两车相距20千米.
或1.2小时两车相距20千米.


科目:初中数学 来源: 题型:
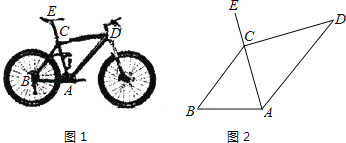
【题目】为倡导“低碳生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图.车架档CD与AD的长分别为60cm,75cm,且AC⊥CD,垂足为C,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AC的长;
(2)求车座点E到车架档AB的距离.
(结果精确到 1cm.参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75≈3.7321)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级(1)班要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”,为此,数学老师对两位同学进行了辅导,并在辅导期间测验了6次,测验成绩如下表(单位:分):
次数,1, 2, 3, 4, 5, 6
甲:79,78,84,81,83,75
乙:83,77,80,85,80,75
利用表中数据,解答下列问题:
(1)计算甲、乙测验成绩的平均数.
(2)写出甲、乙测验成绩的中位数.
(3)计算甲、乙测验成绩的方差.(结果保留小数点后两位)
(4)根据以上信息,你认为老师应该派甲、乙哪名学生参赛?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=4,BC=8,D,E是AB和BC上的动点,连接CD,DE则CD+DE的最小值为( )
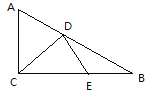
A. 8 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有a个除颜色外完全相同的红球和白球,其中红球有b个,将盒中的球摇匀后从中任意摸出1个球,记录颜色后将球放回盒中,重复进行这过程,如表记录了某班一次摸球实验情况:
摸球总数n | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
摸到红球数m | 325 | 1336 | 3203 | 6335 | 8073 | 12628 |
摸到红球的频率(精确到0.001) | 0.813 | 0.891 | 0.915 | 0.905 | 0.897 | 0.902 |
(1)由此估计任意摸出1个球为红球的概率约是 (精确到0.1)
(2)实验结束后,小明发现了一个一般性的结论:盒子中共有a个球,其中红球有b个,则摇匀后从中任意摸出1个球为红球的概率P可以表示为![]() ,这个结论也得到了老师的证实根据小明的发现,若在该盒子中再放入除颜色外与原来的球完全相同的2个红球和2个白球,摇匀后从中任意摸出1个球为红球的概率为P’,请通过计算比较P与P'的大小.
,这个结论也得到了老师的证实根据小明的发现,若在该盒子中再放入除颜色外与原来的球完全相同的2个红球和2个白球,摇匀后从中任意摸出1个球为红球的概率为P’,请通过计算比较P与P'的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
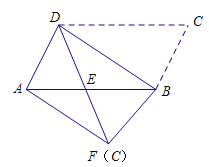
(1)求证:![]() ;
;
(2)判断AF与BD是否平行,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
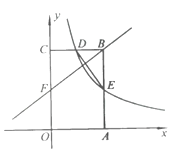
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)直接写出k的值及点E的坐标;
(2)若点F是OC边上一点,且FB⊥DE,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
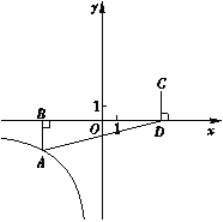
【题目】如图,在平面直角坐标系xOy中,函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
(1)求m,n的值;
(2)若直线![]() (k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当
(k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当![]() 时,求点F的坐标.
时,求点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com