
【题目】如图,A,B分别是数轴上两点,点O为原点,点A表示的数为﹣60,点B表示的数为30.现有两个动点P、Q均从点A出发,沿数轴正方向移动,点P的速度为6单位/秒,点Q的速度为3单位/秒.
(1)若两动点同时出发,当点P到达点B时,点Q在数轴上表示的数为_____;
(2)若点P出发2秒钟后点Q出发,当点P到达点B时,P、Q两点同时停止运动,设点P运动的时间为t秒,运动过程中点P表示的数为x,点Q表示的数为y,求t为何值时,|y|=2|x|.
(3)在(1)的条件下,若点P到达点B停留5秒后以5单位/秒的速度匀速沿数轴向点A运动,求在整个运动过程中当t为何值时,P,Q两点相距20个单位长度.
【答案】(1)-15;(2) 当t=6或![]() 秒时,|y|=2|x|;(3) 在整个运动过程中当t为
秒时,|y|=2|x|;(3) 在整个运动过程中当t为![]() 、
、![]() 或
或![]() 秒时,P,Q两点相距20个单位长度
秒时,P,Q两点相距20个单位长度
【解析】
(1)根据点A、B表示的数可得出线段AB的长度,利用时间=路程÷速度可求出当点P到达点B时点P、Q运动的时间,再由点Q的出发点、速度及运动时间可得出当点P到达点B时点Q在数轴上表示的数;
(2)找出当运动时间为t秒时x、y的值,结合|y|=2|x|即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
(3)分析整个运动过程,由点P的运动速度不同可分三段考虑:当0≤t≤15时,找出点P、Q表示的数,由线段PQ=20可得出关于t的一元一次方程,解之即可得出t值;当15<t≤20时,找出点P、Q表示的数,由线段PQ=20可得出关于t的一元一次方程,解之即可得出t值;当t>20时,找出点P、Q表示的数,由线段PQ=20可得出关于t的一元一次方程,解之即可得出t值.综上即可得出结论.
解:(1)∵点A表示的数为﹣60,点B表示的数为30,
∴线段AB的长度为30﹣(﹣60)=90,
∴当点P到达点B时,点P、Q运动的时间为90÷6=15(秒),
∴当点P到达点B时,点Q在数轴上表示的数为﹣60+3×15=﹣15.
故答案为:﹣15.
(2)当点P运动的时间为t秒时,x=6t﹣60,y=3(t﹣2)﹣60=3t﹣66.
∵|y|=2|x|,即|3t﹣66|=2|6t﹣60|,
解得:t1=6,t2=![]() .
.
答:当t=6或![]() 秒时,|y|=2|x|.
秒时,|y|=2|x|.
(3)∵90÷6=15(秒),15+5=20(秒),
∴分三种情况考虑:
①当0≤t≤15时,点P表示的数为6t﹣60,点Q表示的数为3t﹣60,
∴6t﹣60﹣(3t﹣60)=20,
解得:t=![]()
②当15<x≤20时,点P表示的数为30,点Q表示的数为3t﹣60,
∴30﹣(3t﹣60)=20,
解得:t=![]() (不合题意,舍去);
(不合题意,舍去);
当t>20时,点P表示的数为30﹣5(t﹣20),点Q表示的数为3t﹣60,
∴|30﹣5(t﹣20)﹣(3t﹣60)|=20,
解得:t1=![]() ,t2=
,t2=![]() .
.
综上所述:在整个运动过程中当t为![]() 、
、![]() 或
或![]() 秒时,P,Q两点相距20个单位长度.
秒时,P,Q两点相距20个单位长度.


科目:初中数学 来源: 题型:
【题目】下列条件,不能判定△ABC与△DEF相似的是( )
A.∠C=∠F= ![]() ,∠A=
,∠A= ![]() ,∠D=
,∠D= ![]()
B.∠C=∠F= ![]() ,AB=10,BC=6,DE=15,EF=9
,AB=10,BC=6,DE=15,EF=9
C.∠C=∠F= ![]() ,
, ![]()
D.∠B=∠E= ![]() ,
, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 ;
(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?
(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点,点A在点B的左侧.
(1)求A,B两点的坐标和此抛物线的对称轴;
(2)设此抛物线的顶点为C,点D与点C关于x轴对称,求四边形ACBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①) 
阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径.
(1)再次阅读后,发现AB=寸,CD=寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件.
(2)帮助小智求出⊙O的直径 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出,0<x<4时,直接写出y的取值范围;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,求出矩形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
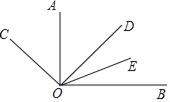
A. 113° B. 134° C. 136° D. 144°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( ) 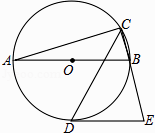
A.![]()
B.2
C.2 ![]()
D.3 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com