
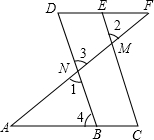
 在横线上填出正确的结论,括号内写上理由已知:∠1=∠2,∠A=∠F.求证:∠C=∠D.
在横线上填出正确的结论,括号内写上理由已知:∠1=∠2,∠A=∠F.求证:∠C=∠D. 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
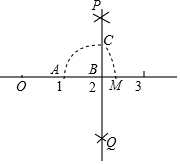 如图,数轴上点A、B对应的数分别是1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径作圆弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,当点M在点B的右侧时,点M对应的数是$\sqrt{5}$.
如图,数轴上点A、B对应的数分别是1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径作圆弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,当点M在点B的右侧时,点M对应的数是$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
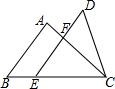 如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=6,EF=4,则DF的长是( )
如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=6,EF=4,则DF的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
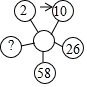 如图,从左上角标注2的圆圈开始,顺时针方向按an+b的规律,(n表示前一个圆圈中的数字,a,b是常数)转换后得到下一个圆圈中的数,则标注“?”的圆圈中的数应是( )
如图,从左上角标注2的圆圈开始,顺时针方向按an+b的规律,(n表示前一个圆圈中的数字,a,b是常数)转换后得到下一个圆圈中的数,则标注“?”的圆圈中的数应是( )| A. | 119 | B. | 120 | C. | 121 | D. | 122 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则$\frac{GH}{EF}$的值是( )
如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则$\frac{GH}{EF}$的值是( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com