
 y与x的函数图象如图所示,当0≤x≤100时,y与x的函数关系式为y=100x;当x>100时,y与x的函数关系式为y=60x+4000.
y与x的函数图象如图所示,当0≤x≤100时,y与x的函数关系式为y=100x;当x>100时,y与x的函数关系式为y=60x+4000. 分析 设长函数的解析式,然后把点的坐标代入,利用待定系数法即可求得.
解答 解:设当0≤x≤100时,y与x的函数关系式为y=mx,
根据图象知;经过点(100,10000),
∴10000=100m,
解得m=100
∴y与x的关系式为:y=100x(0≤x≤100),
当x>100时,设函数关系式为y=kx+b
根据图象知:经过点(100,10000)和(200,16000)
∴$\left\{\begin{array}{l}{100k+b=10000}\\{200k+b=16000}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=60}\\{b=4000}\end{array}\right.$
∴y与x的函数关系式:y=60x+4000(x>100)
故答案为y=100x、y=60x+4000.
点评 本题考查了待定系数法一次函数的解析式,熟练掌握待定系数法是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 总体 | B. | 个体 | C. | 样本 | D. | 样本容量 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
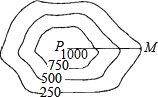 测量队为了测量某地区山顶P的海拔,选择M点作为观测点,从M点测得山顶P的仰角为30°,在比例尺为1:50000的该地区等高线地形图上,量得这两点间的图上距离为3cm,则山顶P的海拔为1116m.($\sqrt{3}$≈1.732)
测量队为了测量某地区山顶P的海拔,选择M点作为观测点,从M点测得山顶P的仰角为30°,在比例尺为1:50000的该地区等高线地形图上,量得这两点间的图上距离为3cm,则山顶P的海拔为1116m.($\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 人数 | 平均身高(单位:厘米) | 方差 | |
| 男生 | 15 | 175 | 36 |
| 女生 | 15 | 165 | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com