
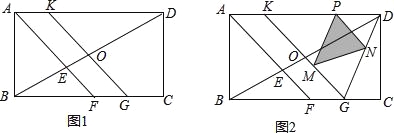
【题目】.如图1,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
(1)求证:①△DOK≌△BOG;②AB+AK=BG;
(2)若KD=KG,BC=4﹣.
①求KD的长度;
②如图2,点P是线段KD上的动点(不与点D、K重合),PM∥DG交KG于点M,PN∥KG交DG于点N,设PD=m,当S△PMN=![]() 时,求m的值.
时,求m的值.
【答案】(1)证明见解析;(2)①2,②1.
【解析】
试题分析:(1)①根据AAS可判定△DOK≌△BOG,②易证四边形AFGK为平行四边形,从而得到AK=FG,而AB=BF,所以AB+AK=BG;(2)①由(1)可知AB=BF,∴AF=KG=DK=BG=AB,AK=FG=AB-AB,再利用AK+DK=AD=BC可求得AB的长,DK长度可求出,②过点G作GI⊥KD,求得S△DKG的值,再根据四边形PMGN是平行四边形,以及△DKG∽△PKM∽△DPN,求得S△DPN和S△PKM的表达式,最后根据等量关系S平行四边形PMGN=S△DKG﹣S△DPN﹣S△PKM,列出关于m的方程,求得m的值即可.
试题解析:(1)①∵在矩形ABCD中,AD∥BC,∴∠KDO=∠GBO,∠DKO=∠BGO.∵点O是BD的中点,∴DO=BO
∴△DOK≌△BOG(AAS).②∵四边形ABCD是矩形,∴∠BAD=∠ABC=90°,AD∥BC
又∵AF平分∠BAD,∴∠BAF=∠BFA=45°,∴AB=BF.∵OK∥AF,AK∥FG,∴四边形AFGK是平行四边形.∴AK=FG.
∵BG=BF+FG,∴BG=AB+AK;(2)①由(1)得,四边形AFGK是平行四边形.∴AK=FG,AF=KG,又∵△DOK≌△BOG,且KD=KG.∴AF=KG=KD=BG.设AB=a,则AF=KG=KD=BG=a.∴AK=FG=BG-BF=a-a,∵AK+DK=AD=BC,∴a-a+a=4-,解得a=.∴KD=a=2.②过点G作GI⊥KD于点I.由(2)①可知KD=AF=2,∴GI=AB=
∴S△DKG=×2×=.∵PD=m,∴PK=2﹣m.∵PM∥DG,PN∥KG,∴四边形PMGN是平行四边形,△DKG∽△PKM∽△DPN.∴ ,即S△DPN=()2 .同理S△PKM=()2 .∵S△PMN=
,即S△DPN=()2 .同理S△PKM=()2 .∵S△PMN=![]() .∴S平行四边形PMGN=2S△PMN=2×
.∴S平行四边形PMGN=2S△PMN=2×![]() =
=![]() .又∵S平行四边形PMGN=S△DKG﹣S△DPN﹣S△PKM.∴
.又∵S平行四边形PMGN=S△DKG﹣S△DPN﹣S△PKM.∴ ,即m2-2m+1=0,解得m1=m2=1.
,即m2-2m+1=0,解得m1=m2=1.
∴当S△PMN=![]() 时,m的值为1.
时,m的值为1.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为________厘米/秒.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3时,求线段DH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1250元,那么衬衫的单价降了多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com