
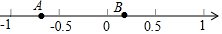 如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )
如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )| A. | 甲、乙 | B. | 甲、丙 | C. | 丙、丁 | D. | 乙、丁 |
分析 根据图示,可得0<b<$\frac{1}{2}$,-1<a<-$\frac{1}{2}$,|a|>|b|,利用特殊值法进行判断.
解答 解:∵0<b<$\frac{1}{2}$,-1<a<-$\frac{1}{2}$,|a|>|b|,
令a=-0.7,b=0.2
则-ab=0.14<$\frac{1}{2}$;a+b=-0.7+0.2=-0,5>-1;-a=0.7>b=0.2,$\frac{a}{b}=\frac{-0.7}{0.2}=-3.5$<-2.
故正确的是甲、乙.
故选A.
点评 此题主要考查了数的绝对值、数的加减乘除运算及数的大小比较.利用特殊值法非常简单.解答此题的关键是根据数轴,给出合理的a、b的值.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 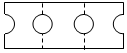 | B. | 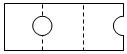 | C. | 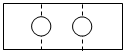 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
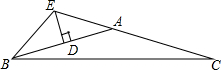 如图,△ABC中,AB=AC,AB的垂直平分线交AB于点D,交CA的延长线于点E,∠EBC=42°,则∠BAC=( )
如图,△ABC中,AB=AC,AB的垂直平分线交AB于点D,交CA的延长线于点E,∠EBC=42°,则∠BAC=( )| A. | 159° | B. | 154° | C. | 152° | D. | 138° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
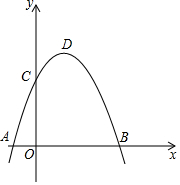 如图,抛物线y=-x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.
如图,抛物线y=-x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3{a^2}}$ | B. | $\sqrt{11a}$ | C. | $\sqrt{12}$ | D. | $\sqrt{\frac{1}{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,将两张等宽的长方形条交叉叠放,重叠部分是一个四边形ABCD,若AD=4cm,∠ABC=30°,则四边形ABCD的面积是8cm2.
如图所示,将两张等宽的长方形条交叉叠放,重叠部分是一个四边形ABCD,若AD=4cm,∠ABC=30°,则四边形ABCD的面积是8cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com