
| x | 0 | 1 | 2 | 3 | 4 |
| y | 3 | 0 | -2 | 0 | 3 |
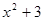 B. y=x2-4x+3 C.
B. y=x2-4x+3 C.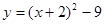 D.
D.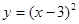
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源:不详 题型:解答题
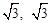 ),对称轴为直线
),对称轴为直线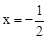 ,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=
,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=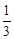 MP,MD=
MP,MD=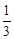 OM,OE=
OM,OE=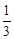 ON,NF=
ON,NF=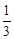 NP.
NP.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.24米 | B.12米 | C.12 米 米 | D.11米 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
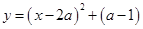 (
( 为常数),当
为常数),当 取不同的值时,其图象构成一个“抛物线系”.下图分别是当
取不同的值时,其图象构成一个“抛物线系”.下图分别是当 ,
, ,
,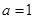 ,
, 时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是
时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是 __________________.
__________________.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
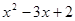 >0.解:令y=
>0.解:令y=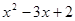 ,画出y=
,画出y=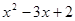 如图所示,
如图所示,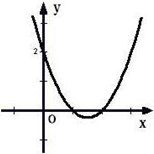
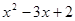 >0的解集为x<1或x>2.
>0的解集为x<1或x>2.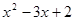 <0的解集为 ;
<0的解集为 ;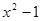 >0的解集为 ;
>0的解集为 ;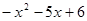 >0.
>0.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为( ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com