
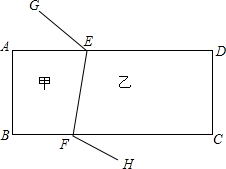
 如图所示,有一块长方形土地ABCD,分别被甲、乙两人承包,一条公路GEFH穿过这块地,为发展经济,决定将这条公路尽量修直,为不影响甲、乙两家土地面积,请你设计一种方案来解决这个问题.
如图所示,有一块长方形土地ABCD,分别被甲、乙两人承包,一条公路GEFH穿过这块地,为发展经济,决定将这条公路尽量修直,为不影响甲、乙两家土地面积,请你设计一种方案来解决这个问题.  A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 作图题(注意:1、标明点;2、线画直;3、结论)
作图题(注意:1、标明点;2、线画直;3、结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
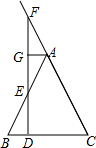 如图,在△ABC中,AB=AC,D是底边BC上的一个动点,过点D作BC的垂线分别交一腰和另一腰的延长线于点E、F,过点A作AG⊥DF于点G.求证:AE=AF.
如图,在△ABC中,AB=AC,D是底边BC上的一个动点,过点D作BC的垂线分别交一腰和另一腰的延长线于点E、F,过点A作AG⊥DF于点G.求证:AE=AF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com