
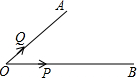
 如图,在∠AOB=30°的两边上有两点P和Q在运动,且点P从离点O有1厘米远的地方出发,以1厘米每秒运动,点Q从点O出发以2厘米每秒运动,则△POQ为等腰三角形时,两点的运动时间为( )秒.
如图,在∠AOB=30°的两边上有两点P和Q在运动,且点P从离点O有1厘米远的地方出发,以1厘米每秒运动,点Q从点O出发以2厘米每秒运动,则△POQ为等腰三角形时,两点的运动时间为( )秒.| A. | $1;2\sqrt{3}+3;\frac{{2\sqrt{3}+1}}{11}$ | B. | $1;2\sqrt{3}+3;\frac{{2\sqrt{3}+1}}{13}$ | C. | $1;2\sqrt{3}+3$;5 | D. | 以上都不对 |
分析 分三种情况:①当OQ=OP时,根据题意列出方程2t=1+t,②当PQ=OP时,解直角三角形得出则t+1=$\sqrt{3}$•2t,③当PQ=OP时,解直角三角形得出OQ=$\sqrt{3}$OP,则2t=$\sqrt{3}$(1+t),然后解方程求出t的值即可.
解答 解:①当OQ=OP时,则2t=1+t,
解得t=1,
②当OQ=PQ时,
∵∠AOB=30°,
∴OP=$\sqrt{3}$OQ,
则t+1=$\sqrt{3}$•2t,
解得t=$\frac{2\sqrt{3}+1}{11}$,
③当PQ=OP时,
∵∠AOB=30°,
∴OQ=$\sqrt{3}$OP,
则2t=$\sqrt{3}$(1+t),
解得t=2$\sqrt{3}$+3,
故选A.
点评 本题考查了等腰三角形的判定以及解直角三角形,注意分类讨论.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
 如图,已知数轴上点A,B是数轴上的一点,AB=12,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A,B是数轴上的一点,AB=12,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.求证:
如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直角△ABC中,∠BAC=90°,AB=AC,BD=CD,BE平分∠ABC,FD⊥ED交AB于F,BE交AD于H,则下列结论:①AH=AE;②S四边形AFDE=$\frac{1}{2}$S△ABC;③BF2+CE2=EF2,其中正确的是( )
如图,直角△ABC中,∠BAC=90°,AB=AC,BD=CD,BE平分∠ABC,FD⊥ED交AB于F,BE交AD于H,则下列结论:①AH=AE;②S四边形AFDE=$\frac{1}{2}$S△ABC;③BF2+CE2=EF2,其中正确的是( )| A. | ①②③ | B. | ②③ | C. | ①② | D. | ①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -x2,$\frac{1}{2}$x,1 | B. | -x2,-$\frac{1}{2}$x,-1 | C. | x2,$\frac{1}{2}$x,1 | D. | 以上答案都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com