
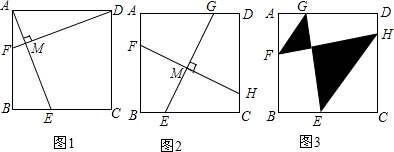
分析 (1)由正方形的性质得AB=DA,∠ABE=90°=∠DAH.所以∠HAO+∠OAD=90°,又知∠ADO+∠OAD=90°,所以∠HAO=∠ADO,于是△ABE≌△DAH,可得AE=DH;
(2)EF=GH.将FE平移到AM处,则AM∥EF,AM=EF,将GH平移到DN处,则DN∥GH,DN=GH.根据(1)的结论得AM=DN,所以EF=GH;
(3)易得△AHF∽△CGE,所以$\frac{AF}{CE}=\frac{FH}{EG}=\frac{FO}{OE}=\frac{1}{2}$,由EC=2得AF=1,过F作FP⊥BC于P,根据勾股定理得EF=$\sqrt{17}$,因为FH∥EG,所以$\frac{FO}{FE}=\frac{HO}{HG}$,根据(2)①知EF=GH,所以FO=HO,再求得三角形FOH与三角形EOG的面积相加即可.
解答 解:(1)∵四边形ABCD是正方形,∠DMA=90°
∴∠DAE+∠ADF=90°,∠DAE+∠EAB=90°,
∴∠ADF=∠EAB
在△DAF和△ABE中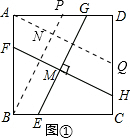
$\left\{\begin{array}{l}{∠ADF=∠EAB}\\{AD=AB}\\{∠BAD=∠B}\end{array}\right.$
∴△DAF≌△ABE,
∴S△ADF=S△ABE=$\frac{1}{2}$•AB•BE=$\frac{1}{2}$×6×2=6;
(2)如图,作AQ∥FH,BP∥EG
则BP=EG,AQ=FH,AQ⊥BP,
∵∠DAQ+∠BAQ=90°,∠ABP+∠BAQ=90°,
∴∠DAQ=∠ABP
在△ABP和△DAQ中
$\left\{\begin{array}{l}{∠DAQ=∠ABP}\\{AB=AD}\\{∠BAD=∠D}\end{array}\right.$
∴△ABP≌△DAQ
∴BP=AQ
∴GE=FH;
(3)∵四边形ABCD是正方形,
∴AB∥CD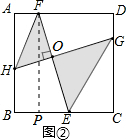
∴∠AHO=∠CGO
∵FH∥EG
∴∠FHO=∠EGO
∴∠AHF=∠CGE
∴△AHF∽△CGE
∴$\frac{AF}{CE}=\frac{FH}{EG}=\frac{FO}{OE}=\frac{1}{2}$
∵EC=2
∴AF=1
过F作FP⊥BC于P,根据勾股定理得EF=$\sqrt{17}$,
∵FH∥EG,
∴$\frac{FO}{FE}=\frac{HO}{HG}$
根据(2)知EF=GH,
∴FO=HO.
∴${S}_{△FOH}=\frac{1}{2}F{O}^{2}=\frac{1}{2}×(\frac{1}{3}EF)^{2}=\frac{17}{18}$
${S}_{△EOG}=\frac{1}{2}E{O}^{2}=\frac{1}{2}×(\frac{2}{3}EF)^{2}=\frac{68}{18}$,
∴阴影部分面积为$\frac{85}{18}$.
点评 本题考查了三角形的综合知识.用到全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等,能够恰当的构造辅助线是解决问题的关键,此类题型综合性较强,难度较大.


科目:初中数学 来源: 题型:填空题
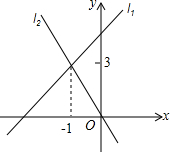 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式0<k2x<k1x+b的解集为-1<x<0.
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式0<k2x<k1x+b的解集为-1<x<0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为2,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为2-$\sqrt{2}$.
如图,正方形ABCD的边长为2,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为2-$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
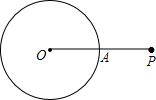 如图,P是⊙O外一点,OP交⊙O于点A,OA=AP.甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下.
如图,P是⊙O外一点,OP交⊙O于点A,OA=AP.甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下.| A. | 甲正确,乙错误 | B. | 乙正确,甲错误 | C. | 两人都正确 | D. | 两人都错误 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
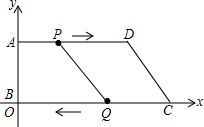 如图,在平面直角坐标系中,O为原点,已知A(0,8),D(24,8),C(26,0),动点P从点A开始沿AD边向点D以1cm/秒的速度运动;动点Q从点C开始沿CO边向点O以3cm/秒的速度运动,若P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.
如图,在平面直角坐标系中,O为原点,已知A(0,8),D(24,8),C(26,0),动点P从点A开始沿AD边向点D以1cm/秒的速度运动;动点Q从点C开始沿CO边向点O以3cm/秒的速度运动,若P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com