
分析 先化简题目中的式子,然后选取合适的值代入化简后的式子即可解答本题,注意x不能取0或1.
解答 解:($\frac{{x}^{2}-1}{{x}^{2}-2x+1}$-$\frac{1}{x-1}$)+$\frac{2}{x}$
=$\frac{{x}^{2}-1-(x-1)}{(x-1)^{2}}+\frac{2}{x}$
=$\frac{{x}^{2}-1-x+1}{(x-1)^{2}}+\frac{2}{x}$
=$\frac{x(x-1)}{(x-1)^{2}}+\frac{2}{x}$
=$\frac{x}{x-1}+\frac{2}{x}$
=$\frac{{x}^{2}+2x-2}{x(x-1)}$
=$\frac{{x}^{2}+2x-2}{{x}^{2}-x}$,
当x=2时,
原式=$\frac{{2}^{2}+2×2-2}{{2}^{2}-2}$=3.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,已知∠ABC=90°,∠ACB=60°,DE是斜边AC的中垂线,分别交AB,AC于点D,E,连接DC,若BD=2,求线段AC的长.
如图,在Rt△ABC中,已知∠ABC=90°,∠ACB=60°,DE是斜边AC的中垂线,分别交AB,AC于点D,E,连接DC,若BD=2,求线段AC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠A=36°,线段AB=6.
如图,已知∠A=36°,线段AB=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
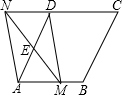 如图,在菱形ABCD中,AB=20,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
如图,在菱形ABCD中,AB=20,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,三个完全相同的小长方形沿“横--竖--横”排列在一个边长分别为5.7cm,4.5cm的大长方形中,图中一个小长方形的周长等于6.8cm.
如图,三个完全相同的小长方形沿“横--竖--横”排列在一个边长分别为5.7cm,4.5cm的大长方形中,图中一个小长方形的周长等于6.8cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com