
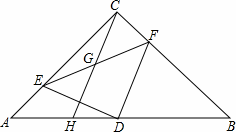
已知,△ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,延长CG交AB于点H.
(1)若E在边AC上.①试说明DE=DF;②试说明CG=GH;
(2)若AE=3,CH=5.求边AC的长.
解:(1)①连接CD,

∵∠ACB=90°,D为AB的中点,AC=BC,
∴CD=AD=BD,
又∵AC=BC,
∴CD⊥AB,
∴∠EDA+∠EDC=90°,∠DCF=∠DAE=45°,
∵DF⊥DE,
∴∠EDF=∠EDC+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中
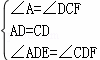
∴△ADE≌△CDF,
∴DE=DF.
②连接DG,
∵∠ACB=90°,G为EF的中点,
∴CG=EG=FG,
∵∠EDF=90°,G为EF的中点,
∴DG=EG=FG,
∴CG=DG,
∴∠GCD=∠CDG
又∵CD⊥AB,
∴∠CDH=90°,
∴∠GHD+∠GCD=90°,∠HDG+∠GDC=90°,
∴∠GHD=∠HDG,
∴GH=GD,
∴CG=GH.
(2)如图,当E在线段AC上时,

∵CG=GH=EG=GF,
∴CH=EF=5,
∵△ADE≌△CDF,
∴AE=CF=3,
∴在Rt△ECF中,由勾股定理得:![]() ,
,
∴AC=AE+EC=3+4=7;
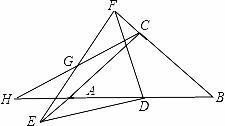
如图,当E在线段CA延长线时,
AC=EC﹣AE=4﹣3=1,
综合上述AC=7或1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3 |
| 4 |
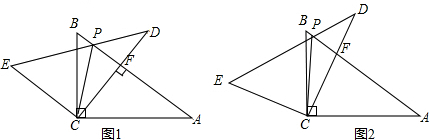
| 25 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.查看答案和解析>>
科目:初中数学 来源: 题型:
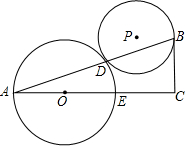 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com