
【题目】一方有难,八方支援.已知甲、乙两地急需一批物资,其中甲地需要240吨,乙地需要260吨.A、B两城市通过募捐,很快筹集齐了这种物资,其中A城市筹到物资200吨,B城市筹到物资300吨.已知从A、B两城市将每吨物资分别运往甲、乙两地所需运费成本(单位:元/吨)如表所示.问:怎样调运可使总运费最少?最少运费为多少元?
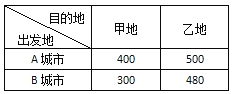
【答案】A城市运往乙地200吨物资,B城市运往甲地240吨物资,B城市运往乙地60吨物资,运费最少为200800元.
【解析】
设A城市运往甲地x吨物资(0≤x≤200),总运费为W元,根据题意,列出一次函数解析式,根据一次函数的性质,即可得到结论.
设A城市运往甲地x吨物资(0≤x≤200),总运费为W元,则:
W=400x+500(200-x)+300(240-x)+480[300-(240-x)]
=80x+200800
∵k=80>0,
∴W随着x的增大而增大,
∴x=0时,W取得最小值为200800元.
答:A城市运往乙地200吨物资,B城市运往甲地240吨物资,B城市运往乙地60吨物资,运费最少为200800元.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
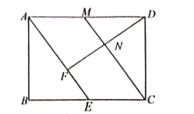
【题目】如图,在矩形![]() 中,点E为
中,点E为![]() 的中点,连接
的中点,连接![]() ,过点D作
,过点D作![]() 于点F,过点C作
于点F,过点C作![]() 于点N,延长
于点N,延长![]() 交
交![]() 于点M.
于点M.
(1)求证:![]()
(2)连接CF,并延长CF交AB于G
①若![]() ,求
,求![]() 的长度;
的长度;
②探究当![]() 为何值时,点G恰好为AB的中点.
为何值时,点G恰好为AB的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年 3 月 12 日植树节期间, 学校预购进 A、B 两种树苗,若购进 A种树苗 3 棵,B 种树苗 5 棵,需 2100 元,若购进 A 种树苗 4 棵,B 种树苗 10棵,需 3800 元.
(1)求购进 A、B 两种树苗的单价;
(2)若该单位准备用不多于 8000 元的钱购进这两种树苗共 30 棵,求 A 种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨![]() 元(
元(![]() 为非负整数),每个月的销售利润为
为非负整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(2)利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
(3)利用函数关系式求出每件商品的售价定为多少元时,每个月的利润恰好是1920元?这时每件商品的利润率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.

(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象,下列结论:①2a>b;②a﹣b+c>0;③a<b;④a>c,其中正确的结论是( )
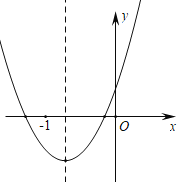
A.①③B.②③C.①④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题]小明在学习时遇到这样一个问题:求不等式x3+3x2﹣x﹣3>0的解集.
他经历了如下思考过程:
[回顾]
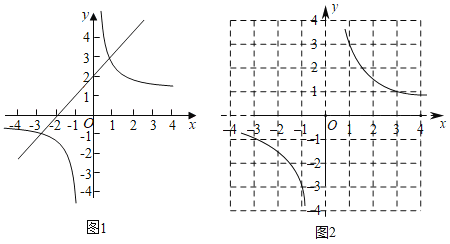
(1)如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>
交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>![]() 的解集是 .
的解集是 .
[探究]将不等式x3+3x2﹣x﹣3>0按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,不等式两边同除以x并移项转化为x2+3x﹣1>![]() ;
;
当x<0时,不等式两边同除以x并移项转化为x2+3x﹣1<![]() .
.
(2)构造函数,画出图象:
设y3=x2+3x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象;
,在同一坐标系中分别画出这两个函数的图象;
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
(3)确定两个函数图象公共点的横坐标:
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 .
[解决]
(4)借助图象,写出解集:
结合“探究”中的讨论,观察两个函数的图象可知:不等式x3+3x2﹣x﹣3>0的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批货物准备运往某地,有甲、乙、丙三辆卡车可雇用.已知甲、乙、丙三辆车每次运货量不变,且甲、乙两车单独运完这批货物分别用![]() 次;甲、丙两车合运相同次数,运完这批货物,甲车共运
次;甲、丙两车合运相同次数,运完这批货物,甲车共运![]() 吨;乙、丙两车合运相同次数,运完这批货物乙车共运
吨;乙、丙两车合运相同次数,运完这批货物乙车共运![]() 吨,现甲、乙、丙合运相同次数把这批货物运完,货主应付甲车主的运费为___________ 元.(按每吨运费
吨,现甲、乙、丙合运相同次数把这批货物运完,货主应付甲车主的运费为___________ 元.(按每吨运费![]() 元计算)
元计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
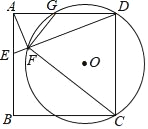
【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com