
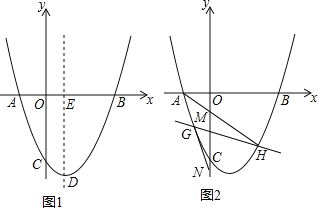
【题目】如图1,在平面直角坐标系中,抛物线y=ax2﹣4ax﹣6(a>0)与x轴交于A,B两点,且OB=3OA,与y轴交于点C,抛物线的顶点为D,对称轴与x轴交于点E.
(1)求该抛物线的解析式,并直接写出顶点D的坐标;
(2)如图2,直线y=![]() +n与抛物线交于G,H两点,直线AH,AG分别交y轴负半轴于M,N两点,求OM+ON的值;
+n与抛物线交于G,H两点,直线AH,AG分别交y轴负半轴于M,N两点,求OM+ON的值;
(3)如图1,点P在线段DE上,作等腰△BPQ,使得PB=PQ,且点Q落在直线CD上,若满足条件的点Q有且只有一个,求点P的坐标.
【答案】(1)y=![]() (x﹣2)2﹣8,D(2,﹣8)(2)9;(3)P(2,8﹣4
(x﹣2)2﹣8,D(2,﹣8)(2)9;(3)P(2,8﹣4![]() )
)
【解析】
(1)由OB=3OA可设A(-t,0),B(3t,0),代入抛物线解析式即得到关于a、t的二元方程,解方程求出a即求得抛物线解析式,配方即得到顶点D的坐标.
(2)由(1)求得t=2可知点A(-2,0),设G(x1,![]() x12-2x1-6),H(x2,
x12-2x1-6),H(x2,![]() x22-2x2-6),把直线y=
x22-2x2-6),把直线y=![]() x+n与抛物线解析式联立方程组,消去y后整理得关于x的一元二次方程,x1、x2即为方程的解,根据韦达定理求得x1+x2=3.设直线AG解析式为y=kx+b,把点A、G坐标代入求出b的值即为点N纵坐标,进而得到用x1表示的ON的值,同理可求得用x2表示的OM的值,相加再把x1+x2代入即求得OM+ON的值.
x+n与抛物线解析式联立方程组,消去y后整理得关于x的一元二次方程,x1、x2即为方程的解,根据韦达定理求得x1+x2=3.设直线AG解析式为y=kx+b,把点A、G坐标代入求出b的值即为点N纵坐标,进而得到用x1表示的ON的值,同理可求得用x2表示的OM的值,相加再把x1+x2代入即求得OM+ON的值.
(3)以点P为圆心,PB长为半径的⊙P,由于满足PB=PQ(即点Q在⊙P上)且点Q在直线CD上的点Q有且只有一个,即⊙P与直线CD只有一个公共点,所以直线CD与⊙P相切于点Q.由(1)得点C、D坐标可知直线CD与DE夹角为45°,△PDQ为等腰直角三角形,PD=
2 |
PQ=
2 |
PB.设点P纵坐标为p,用p表示PB和PD的长并列得方程即可求p的值.由于点P在线段DE上,故p的值为负数,舍去正数解.
(1)∵抛物线y=ax2﹣4ax﹣6与x轴交于A,B两点,OB=3OA
∴设A(﹣t,0),B(3t,0)(t>0)
∴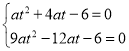 解得:
解得:![]()
∴抛物线解析式为y=![]() x2﹣2x﹣6=
x2﹣2x﹣6=![]() (x﹣2)2﹣8
(x﹣2)2﹣8
∴顶点D的坐标为(2,﹣8)
(2)∵t=2
∴A(﹣2,0)
设抛物线上的点G(x1,![]() x12﹣2x1﹣6),H(x2,
x12﹣2x1﹣6),H(x2,![]() x22﹣2x2﹣6)
x22﹣2x2﹣6)
∵直线y=![]() +n与抛物线交于G,H两点
+n与抛物线交于G,H两点
∴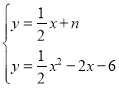 整理得:x2﹣3x﹣12﹣2n=0
整理得:x2﹣3x﹣12﹣2n=0
∴x1+x2=3
设直线AG解析式为y=kx+b,即N(0,b)(b<0)
∴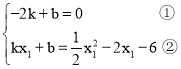
①×x1得:﹣2kx1+bx1=0 ③
②×2得:2kx1+2b=x12﹣4x1﹣12 ④
③+④得:(x1+2)b=(x1+2)(x1﹣6)
∵点G与A不重合,即x1+2≠0
∴b=x1﹣6即ON=﹣b=6﹣x1
同理可得:OM=6﹣x2
∴OM+ON=6﹣x2+6﹣x1=12﹣(x1+x2)=12﹣3=9
(3)如图,过点C作CF⊥DE于点F,以点P为圆心、PB为半径作圆

∵PB=PQ
∴点Q在⊙P上
∵有且只有一个点Q在⊙P上又在直线CD上
∴⊙P与直线CD相切于点Q
∴PQ⊥CD
由(1)得:B(6,0),C(0,﹣6),D(2,﹣8)
∴CF=2,DF=﹣6﹣(﹣8)=2,即CF=DF
∴∠CDF=45°
∴△DPQ为等腰直角三角形
∴PD=![]() PQ
PQ
∴PD2=2PQ2=2PB2
设P(2,p)(﹣8≤p≤0)
∴PD=p+8,PB2=(6﹣2)2+p2=16+p2
∴(p+8)2=16+p2
解得:p1=8﹣4![]() ,p2=8+4
,p2=8+4![]() (舍去)
(舍去)
∴点P坐标为(2,8﹣4![]() )
)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴正半轴上,点A与原点重合,点D的坐标是 (3,4),反比例函数y=![]() (k≠0)经过点C,则k的值为( )
(k≠0)经过点C,则k的值为( )
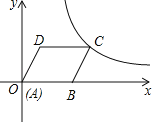
A.12B.15C.20D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E点.

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=![]() (x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为_____.
(x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为_____.
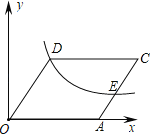
查看答案和解析>>
科目:初中数学 来源: 题型:
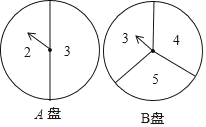
【题目】甲、乙两同学玩转盘游戏时,把质地相同的两个盘A、B分别平均分成2份和3份,并在每一份内标有数字如图.游戏规则:甲、乙两同学分别同时转动两个转盘各1次,当转盘停止后,指针所在区域的数字之积为偶数时甲胜;数字之积为奇数时乙胜.若指针恰好在分割线上,则需要重新转动转盘.
(1)用树状图或列表的方法,求甲获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
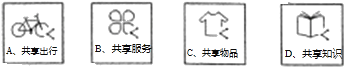
【题目】从共享单车、共享汽车等共享出行到共享充电宝、共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速普及应用,越来越多的企业与个人成为参与者与受益者,小宇上网查阅了相关资料,顺便收集到四个共享经济领域的图标,并将其制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同),将这四张卡片背面朝上,洗匀放好.
(1)从中随机抽取一张,求刚好抽到“共享服务”的概率.
(2)从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号A,B,C,D表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司购进10 000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如下表:
苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为_____(结果保留小数点后一位),损坏的苹果约有______kg.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com