Question

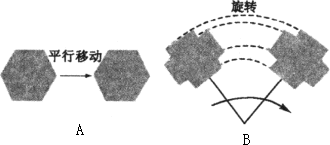
我们知道，对于两个图形，如果沿一条直线对折后，它们能完全重合，那么这两个图形成轴对称，既然成轴对称的两个图形能够完全重合，那么“关于某条直线对称的两个图形是全等形”。通常把图形从一种情况到另一种情况的对应关系称作图形变换，对称就是一种变换，观察图①、②容易看出，经过图形变换后，变换前后图形的位置改变了，但它的形状和大小并没有改变，这种只改变图形的位置，而不改变其形状、大小的图形变换叫做全等变换，前面说到的对称变换是一种全等变换，图①、②所示的变换分别是平移变换和旋转变换，它们都是全等变换。
请你回答：全等变换的两个图形面积相等吗？为什么？

Answer 1

解：全等变换的两个图形面积相等。