
分析 (1)如图连接OE.由$\widehat{AE}$=$\widehat{BE}$,推出OE⊥AB,由CD⊥AB,推出CD∥OE,推出∠E=∠DCE,由OE=OC,推出∠E=∠ECO,推出∠ECD=∠ECO,即可解决问题.
(2)延长CO交⊙O于P,连接AP、AE、OE.首先证明AP∥EK,推出∠PAE=∠AEK,由∠PAE=∠PCE,∠PCE=∠ECG,推出∠AEH=∠CEG,推出$\widehat{AH}$=$\widehat{EG}$,推出AH=EG即可.
(3)连接BC、PA、PE、AE、EB、CH,作PF⊥EM于F,EJ⊥CB交CB的延长线于J.首先证明HN=AP=KF,想办法证明AK=PF=BJ=1,利用勾股定理求出EF=KH=2,由△AKH∽△EKC,得到AK•KC=HK•KE,设HN=AP=KF=x,可得方程1×16=2(x+2),解得x=6,延长即可解决问题.
解答 (1)证明:如图连接OE.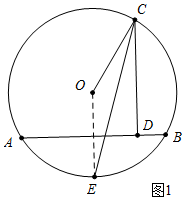
∵$\widehat{AE}$=$\widehat{BE}$,
∴OE⊥AB,∵CD⊥AB,
∴CD∥OE,
∴∠E=∠DCE,
∵OE=OC,
∴∠E=∠ECO,
∴∠ECD=∠ECO,
∴EC平分∠OCD.
(2)证明:延长CO交⊙O于P,连接AP、AE、OE.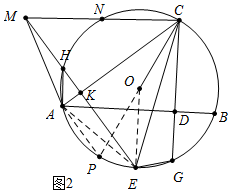
∵PC是直径,
∴∠CAP=90°,
∵E、M关于AC对称,
∴AC⊥EM,
∴∠CKE=∠CAP=90°,
∴PA∥KE,
∴∠PAE=∠AEK,
∵∠PAE=∠PCE,∠PCE=∠ECG,
∴∠AEH=∠CEG,
∴$\widehat{AH}$=$\widehat{EG}$,
∴AH=EG.
(3)解:连接BC、PA、PE、AE、EB、CH,作PF⊥EM于F,EJ⊥CB交CB的延长线于J.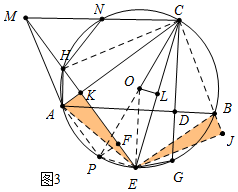
∵E、M关于AC对称,
∴∠MCA=∠ECA,∵∠HCA=∠PCE,
∴∠ACP=∠HCN,
∴$\widehat{NH}$=$\widehat{AP}$,
∴HN=PA,设AP=HN=x,易知四边形AKFP是矩形,
∴AK=PF,AP=KF=x,
∵AH=PE,AK=PF,
∴Rt△AKH≌Rt△PFE,
∴HK=PE,
∵EC=EC,∠ECK=∠ECJ,∠CKE=∠EJC=90°,
∴△CEK≌△CEJ,
∴CK=CJ=16,EK=EJ,
∵AE=EB,
∴Rt△EKA≌Rt△EJB,
∴AK=BJ=PF=CJ-BC=16-15=1,
∵CO=OP,CL=LE,
∴PE=2OL=$\sqrt{5}$,
在Rt△PFE中,HK=EF=$\sqrt{P{E}^{2}-P{F}^{2}}$=2,
由△AKH∽△EKC,得到AK•KC=HK•KE,
∴1×16=2(x+2),
∴x=6,
∴HN=PA=6.
点评 本题考查圆综合题、轴对称变换、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加辅助线,构造全等三角形解决问题,本题比较难,多次应用三角形全等解决问题,属于中考压轴题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 42 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
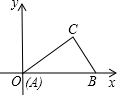 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合.随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.
如图,Rt△ABC中,∠C=90°,AB=10,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合.随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E,现有点A(2,0)和抛物线E上的点B(-1,n),请完成下列任务;
对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E,现有点A(2,0)和抛物线E上的点B(-1,n),请完成下列任务;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
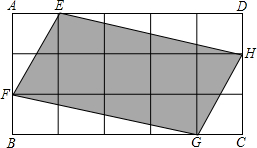 如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点.若四边形EFGH的面积为1,则矩形ABCD的面积为$\frac{5}{3}$.
如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点.若四边形EFGH的面积为1,则矩形ABCD的面积为$\frac{5}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com