
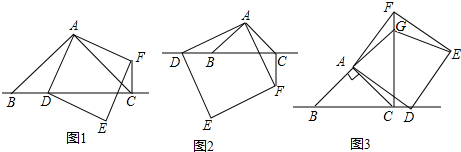
分析 (1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论;②由正方形ADEF的性质可推出△DAB≌△FAC,根据全等三角形的性质得到CF=BD,∠ACF=∠ABD,根据余角的性质即可得到结论;
(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论.
(3)根据等腰直角三角形的性质得到BC=$\sqrt{2}$AB=2$\sqrt{2}$,AH=$\frac{1}{2}$BC=$\sqrt{2}$,求得DH=$\frac{3\sqrt{2}}{2}$,根据正方形的性质得到AD=DE,∠ADE=90°,根据矩形的性质得到NE=CM,EM=CN,由角的性质得到∠ADH=∠DEM,根据全等三角形的性质得到EM=DH=$\frac{3\sqrt{2}}{2}$,DM=AH=$\sqrt{2}$,等量代换得到CN=EM=$\frac{3\sqrt{2}}{2}$,EN=CM=$\frac{3\sqrt{2}}{2}$,根据等腰直角三角形的性质得到CG=BC=2$\sqrt{2}$,根据勾股定理即可得到结论.
解答 解:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,$\left\{\begin{array}{l}{AD=AF}&{\;}\\{∠BAD=∠CAF}&{\;}\\{AB=AC}&{\;}\end{array}\right.$,
∴△DAB≌△FAC(SAS),
∴∠B=∠ACF,
∴∠ACB+∠ACF=90°,即BC⊥CF;
故答案为:垂直;
②△DAB≌△FAC,
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD;
故答案为:BC=CF+CD;
(2)CF⊥BC成立;BC=CD+CF不成立,CD=CF+BC.理由如下:
∵正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,$\left\{\begin{array}{l}{AD=AF}&{\;}\\{∠BAD=∠CAF}&{\;}\\{AB=AC}&{\;}\end{array}\right.$,
∴△DAB≌△FAC(SAS),
∴∠ABD=∠ACF,
∵∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°.
∴∠ABD=180°-45°=135°,
∴∠BCF=∠ACF-∠ACB=135°-45°=90°,
∴CF⊥BC.
∵CD=DB+BC,DB=CF,
∴CD=CF+BC.
(3)解:过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,如图3所示:
∵∠BAC=90°,AB=AC,
∴BC=$\sqrt{2}$AB=2$\sqrt{2}$,AH=$\frac{1}{2}$BC=$\sqrt{2}$,
∴CD=$\frac{1}{4}$BC=$\frac{\sqrt{2}}{2}$,CH=$\frac{1}{2}$BC=$\sqrt{2}$,
∴DH=$\frac{3\sqrt{2}}{2}$,
由(2)证得BC⊥CF,CF=BD=$\frac{5\sqrt{2}}{2}$,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADC=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90°,
∴∠ADH=∠DEM,
在△ADH与△DEM中,$\left\{\begin{array}{l}{∠ADH=∠DEM}&{\;}\\{∠AHD=∠DME}&{\;}\\{AD=DE}&{\;}\end{array}\right.$,
∴△ADH≌△DEM(AAS),
∴EM=DH=$\frac{3\sqrt{2}}{2}$,DM=AH=$\sqrt{2}$,
∴CN=EM=$\frac{3\sqrt{2}}{2}$,EN=CM=$\frac{3\sqrt{2}}{2}$,
∵∠ABC=45°,
∴∠BGC=45°,
∴△BCG是等腰直角三角形,
∴CG=BC=2$\sqrt{2}$,
∴GN=CG-CN=$\frac{\sqrt{2}}{2}$,
∴EG=$\sqrt{G{N}^{2}+E{N}^{2}}$=$\sqrt{(\frac{\sqrt{2}}{2})^{2}+(\frac{3\sqrt{2}}{2})^{2}}$=$\sqrt{5}$.
点评 本题考查了四边形综合题,需要掌握全等三角形的判定和性质,正方形的性质,余角的性质,勾股定理,等腰直角三角形的判定和性质,矩形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:填空题
| 应试者 | 听 | 说 | 读 | 写 |
| 甲 | 85 | 83 | 78 | 75 |
| 乙 | 73 | 80 | 85 | 82 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| 49.5-59.5 | 3 | 0.05 |
| 59.5-69.5 | 9 | m |
| 69.5-79.5 | n | 0.40 |
| 79.5-89.5 | 18 | 0.30 |
| 89.5-99.5 | 6 | p |
| 合计 | q | 1.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
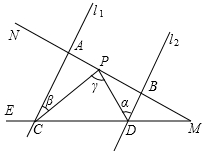 如图,已知 l1∥l2,射线MN分别和直线l1,l2交于A、B,射线ME分别和直线l1,l2交于C、D,点P在A、B间运动(P与A、B两点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
如图,已知 l1∥l2,射线MN分别和直线l1,l2交于A、B,射线ME分别和直线l1,l2交于C、D,点P在A、B间运动(P与A、B两点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x2-6xy=3x(x-2y) | B. | x2-9y2=(x-3y)(x+3y) | ||
| C. | 4x2+4x+1=(2x+1)2 | D. | x2-y2+2y-1=(x+y+1)(x-y-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com