
【题目】如图,已知在正方形ABCD中,AE∥BD,BE=BD,BE交AD于F.求证:DE=DF.
【答案】证明:连接AC,交BD于点O,作EG⊥BD于点G.
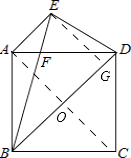
∵四边形ABCD是正方形,
∴AC⊥BD,
∵AE∥BD,
∴四边形AOGE是矩形,
∴EG=AO= ![]() AC=
AC= ![]() BD=
BD= ![]() BE,
BE,
∴∠EBD=30°,
∵∠EBD=30°,BE=BD,
∴∠BED=75°,
∵∠EFD=∠FDB+∠EBD=45+30=75°,
∴∠DEF=∠DFE,
∴DF=DE.
【解析】连接AC,交BD于点O,作EG⊥BD垂足为G,先证明四边形AOGE是矩形,从而可得到EG=![]() BD=
BD=![]() BE,从而可求得∠EBD=30°,接下来可求得∠BED=75°,然后再依据∠EFD=∠FDB+∠EBD求得∠EFD的度数,故∠DEF=∠DFE,最后,依据等边对等角的性质进行证明即可.
BE,从而可求得∠EBD=30°,接下来可求得∠BED=75°,然后再依据∠EFD=∠FDB+∠EBD求得∠EFD的度数,故∠DEF=∠DFE,最后,依据等边对等角的性质进行证明即可.
【考点精析】本题主要考查了等腰三角形的性质和含30度角的直角三角形的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )
A.![]() π
π
B.![]() π
π
C.6π
D.![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日世界读书日这天,滨江初二年级的学生会,就2018年寒假读课外书数量(单位:本)做了调查,他们随机调查了甲、乙两个班的10名同学,调查过程如下
收集数据
甲、乙两班被调查者读课外书数量(单位:本)统计如下:
甲:1,9,7,4,2,3,3,2,7,2
乙:2,6,6,3,1,6,5,2,5,4
整理、描述数据绘制统计表如下,请补全下表:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 4 | 3 | ||
乙 | 6 | 3.2 |
分析数据、推断结论
(1)该校初二乙班共有40名同学,你估计读6本书的同学大概有_____人;
(2)你认为哪个班同学寒假读书情况更好,写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为____________海里/时.
查看答案和解析>>
科目:初中数学 来源: 题型:
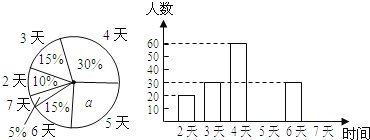
【题目】扬州市教育行政部门为了了解八年级学生每学期参加综合实践活动的情况,随机调查了部分学生,并将他们一学期参加综合实践活动的天数进行统计,绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:
(1)参加调查的八年级学生总人数为_______人;
(2)根据图中信息,补全条形统计图;扇形统计图中“活动时间为4天”的扇形所对应的圆心角的度数为_______;
(3)如果全市共有八年级学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
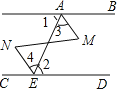
【题目】如图,直线AB,CD被直线AE所截,直线AM,EN被MN所截.请你从以下三个条件:①AB∥CD;②AM∥EN;③∠BAM=∠CEN中选出两个作为已知条件,另一个作为结论,得出一个正确的命题.
(1)请按照:“∵ , ;∴ ”的形式,写出所有正确的命题;
(2)在(1)所写的命题中选择一个加以证明,写出推理过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com