
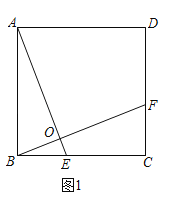
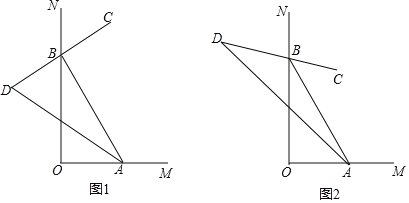
”¾ĢāÄæ”æ ŌŚÕż·½ŠĪABCDÖŠ£®
£Ø1£©ČēĶ¼1£¬µćE”¢F·Ö±šŌŚBC”¢CDÉĻ£¬AE”¢BFĻą½»ÓŚµćO£¬”ĻAOB=90”ć£¬ŹŌÅŠ¶ĻAEÓėBFµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ČēĶ¼2£¬µćE”¢F”¢G”¢H·Ö±šŌŚ±ßBC”¢CD”¢DA”¢ABÉĻ£¬EG”¢FHĻą½»ÓŚµćO£¬”ĻGOH=90”ć£¬ĒŅEG=7£¬ĒóFHµÄ³¤£»
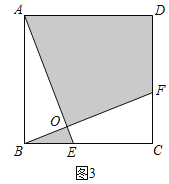
£Ø3£©ČēĶ¼3£¬µćE”¢F·Ö±šŌŚBC”¢CDÉĻ£¬AE”¢BFĻą½»ÓŚµćO£¬”ĻAOB=90”ć£¬ČōAB=5£¬Ķ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ÓėÕż·½ŠĪµÄĆ껿֮±ČĪŖ4£ŗ5£¬Ēó”÷ABOµÄÖܳ¤£®

”¾“š°ø”æ£Ø1£©AE=BF£¬ĄķÓɼū½āĪö£»£Ø2£©FH=7£»£Ø3£©”÷AOBµÄÖܳ¤ĪŖ5+![]()
”¾½āĪö”æ
£Ø1£©ÓÉĖıߊĪABCDŹĒÕż·½ŠĪæɵĆAB=BC£¬”ĻABE=”ĻBCF=90”ć£¬øł¾ŻÓą½ĒµÄŠŌÖŹæɵƔĻBAO=”ĻCBF£¬Č»ŗóøł¾ŻASAæÉÖ¤”÷ABE”Õ”÷BCF£¬½ų¶ųæÉµĆ½įĀŪ£»
£Ø2£©ČēĶ¼4£¬×÷øØÖśĻߣ¬¹¹½ØĘ½ŠŠĖıߊĪAMEGŗĶĘ½ŠŠĖıߊĪBNFH£¬µĆAM=GE£¬BN=FH£¬ÓÉ£Ø1£©ĢāµÄ½įĀŪÖŖ”÷ABM”Õ”÷BCN£¬½ų¶ųæɵĆFHµÄ³¤£»
£Ø3£©øł¾ŻÕż·½ŠĪµÄĆ껿ŗĶŅõÓ°²æ·ÖµÄĆ껿æÉµĆ£ŗæհײæ·ÖµÄĆ껿ĪŖ25£20=5£¬Ņ׵Ɣ÷AOBµÄĆ껿ÓėĖıߊĪOECFµÄĆ껿ĻąµČ£¬ÉčAO=a£¬BO=b£¬ŌņŅ×µĆab=5£¬øł¾Ż¹“¹É¶ØĄķµĆ£ŗa2+b2=52£¬Č»ŗóøł¾ŻĶźČ«Ę½·½¹«Ź½¼“æÉĒó³öa+b£¬½ųŅ»²½¼“µĆ½į¹ū£®
½ā£ŗ£Ø1£©AE=BF£¬ĄķÓÉŹĒ£ŗČēĶ¼1£¬”ßĖıߊĪABCDŹĒÕż·½ŠĪ£¬
”ąAB=BC£¬”ĻABE=”ĻBCF=90”ć£¬
”ß”ĻAOB=90”ć£¬”ą”ĻBAO+”ĻABO=90”ć£¬
Ó֔ߔĻCBF+”ĻABO=90”ć£¬”ą”ĻBAO=”ĻCBF£¬
”ą”÷ABE”Õ”÷BCF£ØASA£©£®
”ąAE=BF£»
£Ø2£©ŌŚĶ¼2ÖŠ£¬¹żµćA×÷AM”ĪGE½»BCÓŚM£¬¹żµćB×÷BN”ĪFH½»CDÓŚN£¬AMÓėBN½»ÓŚµćO”䣬ČēĶ¼4£¬ŌņĖıߊĪAMEGŗĶĖıߊĪBNFH¾łĪŖĘ½ŠŠĖıߊĪ£¬
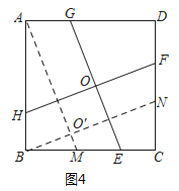
”ąAM=GE£¬BN=FH£¬
”ß”ĻGOH=90”ć£¬AM”ĪGE£¬BN”ĪFH£¬”ą”ĻAO”äB=90”ć£¬
ÓÉ£Ø1£©µĆ£¬”÷ABM”Õ”÷BCN£¬”ąAM=BN£¬
”ąFH=GE=7£»
£Ø3£©ČēĶ¼3£¬”ßŅõÓ°²æ·ÖµÄĆ껿ÓėÕż·½ŠĪABCDµÄĆ껿֮±ČĪŖ4£ŗ5£¬
”ąŅõÓ°²æ·ÖµÄĆ껿ĪŖ![]() ”Į25=20£¬”ąæհײæ·ÖµÄĆ껿ĪŖ25£20=5£¬
”Į25=20£¬”ąæհײæ·ÖµÄĆ껿ĪŖ25£20=5£¬
ÓÉ£Ø1£©µĆ£¬”÷ABE”Õ”÷BCF£¬
”ą”÷AOBµÄĆ껿ÓėĖıߊĪOECFµÄĆ껿ĻąµČ£¬¾łĪŖ![]() ”Į5=
”Į5=![]() £¬
£¬
ÉčAO=a£¬BO=b£¬Ōņ![]() ab=
ab=![]() £¬¼“ab=5£¬
£¬¼“ab=5£¬
ŌŚRt”÷AOBÖŠ£¬”ĻAOB=90”ć£¬”ąa2+b2=52£¬
”ąa2+2ab+b2=25+10=35£¬¼“![]() £¬
£¬
”ąa+b=![]() £¬¼“AO+BO=
£¬¼“AO+BO=![]() £¬
£¬
”ą”÷AOBµÄÖܳ¤ĪŖ5+![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£ŗŅŃÖŖAB=10£¬µćC”¢DŌŚĻ߶ĪABÉĻĒŅAC=DB=2£» PŹĒĻ߶ĪCDÉĻµÄ¶Æµć£¬·Ö±šŅŌAP”¢PBĪŖ±ßŌŚĻ߶ĪABµÄĶ¬²ą×÷µČ±ß”÷AEPŗĶµČ±ß”÷PFB£¬Į¬½įEF£¬ÉčEFµÄÖŠµćĪŖG£»µ±µćP“ÓµćCŌĖ¶Æµ½µćDŹ±£¬ŌņµćGŅʶÆĀ·¾¶µÄ³¤ŹĒ________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,”ĻMON=Ø»£Ø0”ć<Ø»<180”ć£©,µćA.B·Ö±šŌŚOM”¢ONÉĻŌĖ¶Æ(²»ÓėµćOÖŲŗĻ).
(1)ČēĶ¼1,”ĻMON=90”ć£¬BCŹĒ”ĻABNµÄĘ½·ÖĻߣ¬BCµÄ·“·½ĻņŃÓ³¤ĻßÓė”ĻBAOµÄĘ½·ÖĻß½»ÓėµćD.
¢ŁČō”ĻBAO=60”ć,Ōņ”ĻD=___.
¢Ś²ĀĻė£ŗ”ĻDµÄ¶ČŹżŹĒ·ńĖęA£¬BµÄŅĘ¶Æ·¢Éś±ä»Æ?²¢ĖµĆ÷ĄķÓÉ”£
(2)ČēĶ¼2£¬”ĻMON=¦Į(0”ć<¦Į<180”ć)”±,”ĻABC=![]() ”ĻABN,”ĻBAD=
”ĻABN,”ĻBAD=![]() ”ĻBAO,ĘäÓąĢõ¼ž²»±ä,Ōņ”ĻD=___”ć(ÓĆŗ¬¦Į”¢nµÄ“śŹżŹ½±ķŹ¾)
”ĻBAO,ĘäÓąĢõ¼ž²»±ä,Ōņ”ĻD=___”ć(ÓĆŗ¬¦Į”¢nµÄ“śŹżŹ½±ķŹ¾)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ä³½ØÖžĪļAC¶„²æÓŠŅ»ĘģøĖAB£¬ĒŅµćA£¬B£¬CŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬Š”Ć÷ŌŚµŲĆęD“¦¹Ū²āĘģøĖ¶„¶ĖBµÄŃö½ĒĪŖ30”ć£¬Č»ŗóĖūÕż¶Ō½ØÖžĪļµÄ·½ĻņĒ°½ųĮĖ20Ć×µ½“ļµŲĆęµÄE“¦£¬ÓÖ²āµĆĘģøĖ¶„¶ĖBµÄŃö½ĒĪŖ60”ć£¬ŅŃÖŖ½ØÖžĪļµÄø߶ČAC=12m£¬ĒóĘģøĖABµÄøß¶Č£Ø½į¹ū¾«Č·µ½0.1Ć×£©£®²Īæ¼Źż¾Ż£ŗ![]() ”Ö1.73£¬
”Ö1.73£¬![]() ”Ö1.41£®
”Ö1.41£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
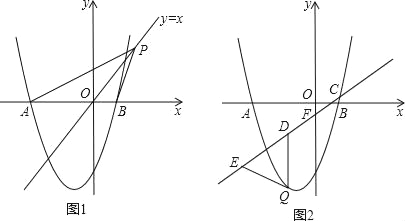
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=ax2+2x©3ÓėxÖį½»ÓŚA”¢BĮ½µć£¬ĒŅB£Ø1£¬0£©
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½ŗĶµćAµÄ×ų±ź£»
£Ø2£©ČēĶ¼1£¬µćPŹĒÖ±Ļßy=xÉĻµÄ¶Æµć£¬µ±Ö±Ļßy=xĘ½·Ö”ĻAPBŹ±£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©ČēĶ¼2£¬ŅŃÖŖÖ±Ļßy=![]() x©
x©![]() ·Ö±šÓėxÖį”¢yÖį½»ÓŚC”¢FĮ½µć£¬µćQŹĒÖ±ĻßCFĻĀ·½µÄÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬¹żµćQ×÷yÖįµÄĘ½ŠŠĻߣ¬½»Ö±ĻßCFÓŚµćD£¬µćEŌŚĻ߶ĪCDµÄŃÓ³¤ĻßÉĻ£¬Į¬½ÓQE£®ĪŹ£ŗŅŌQDĪŖŃüµÄµČŃü”÷QDEµÄĆ껿ŹĒ·ń“ęŌŚ×ī“óÖµ£æČō“ęŌŚ£¬ĒėĒó³öÕāøö×ī“óÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
·Ö±šÓėxÖį”¢yÖį½»ÓŚC”¢FĮ½µć£¬µćQŹĒÖ±ĻßCFĻĀ·½µÄÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬¹żµćQ×÷yÖįµÄĘ½ŠŠĻߣ¬½»Ö±ĻßCFÓŚµćD£¬µćEŌŚĻ߶ĪCDµÄŃÓ³¤ĻßÉĻ£¬Į¬½ÓQE£®ĪŹ£ŗŅŌQDĪŖŃüµÄµČŃü”÷QDEµÄĆ껿ŹĒ·ń“ęŌŚ×ī“óÖµ£æČō“ęŌŚ£¬ĒėĒó³öÕāøö×ī“óÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚµČ±ßČż½ĒŠĪABCÖŠ£¬µćD”¢E·Ö±šŌŚ±ßBC£¬ACÉĻ£¬DE”ĪAB£¬¹żµćE×÷EF”ĶDE£¬½»BCµÄŃÓ³¤ĻßÓŚµćF£¬CD=2£¬ŌņDFµÄ³¤ĪŖ(””””)
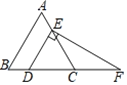
A.2B.3C.4D.5
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅŹŠ¾ŁŠŠ”°µŚŹ®Ęß½ģÖŠŠ”ѧɜŹé·Ø“óČü”±×÷Ę·±ČČü£¬ŅŃÖŖĆæ·ł²ĪČü×÷Ę·³É¼Ø¼ĒĪŖ![]() £¬×éĪÆ»į“Ó1000·łŹé·Ø×÷Ę·ÖŠĖ껜³éČ”ĮĖ²æ·Ö²ĪČü×÷Ę·£¬Ķ³¼ĘĮĖĖüĆĒµÄ³É¼Ø£¬²¢»ęÖĘ³ÉČēĻĀĶ³¼ĘĶ¼±ķ.
£¬×éĪÆ»į“Ó1000·łŹé·Ø×÷Ę·ÖŠĖ껜³éČ”ĮĖ²æ·Ö²ĪČü×÷Ę·£¬Ķ³¼ĘĮĖĖüĆĒµÄ³É¼Ø£¬²¢»ęÖĘ³ÉČēĻĀĶ³¼ĘĶ¼±ķ.
·ÖŹż¶Ī | ʵŹż | °Ł·Ö±Č |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
ŗĻ¼Ę | 100 | 1 |
Źé·Ø×÷Ę·±ČČü³É¼ØʵŹżÖ±·½Ķ¼

øł¾ŻÉĻŹöŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
(1)ĒėÄć°Ń±ķÖŠæհד¦µÄŹż¾ŻĢīŠ“ĶźÕū.
(2)Ēė²¹Č«Źé·Ø×÷Ę·±ČČü³É¼ØʵŹżÖ±·½Ķ¼.
(3)Čō80·Ö(ŗ¬80·Ö)ŅŌÉĻµÄŹé·Ø×÷Ę·½«±»ĘĄĪŖµČ¼¶½±£¬ŹŌ¹Ą¼ĘČ«ŹŠ»ńµĆµČ¼¶µÄ·łŹż.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±ĻßAB”¢CDĻą½»ÓŚµćO£¬”ĻBOC£½80”ć£¬OEŹĒ”ĻBOCµÄ½ĒĘ½·ÖĻߣ¬OFŹĒOEµÄ·“ĻņŃÓ³¤Ļߣ®
£Ø1£©Ēó”Ļ2”¢”Ļ3µÄ¶ČŹż£»
£Ø2£©ĖµĆ÷OFĘ½·Ö”ĻAODµÄĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com