
【题目】如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于点A、B两点,且与反比例函数y=![]() 的图象在第一象限内的部分交于点C,CD垂直于x轴于点D,其中OA=OB=OD=2.
的图象在第一象限内的部分交于点C,CD垂直于x轴于点D,其中OA=OB=OD=2.
(1)直接写出点A、C的坐标;
(2)求这两个函数的表达式;
(3)若点P在y轴上,且S△ACP=14,求点P的坐标.
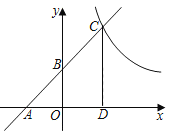
【答案】(1)A点坐标为(﹣2,0),C点坐标为(2,4);(2)反比例函数解析式为y=![]() ,一次函数解析式为y=x+2;(3)点P的坐标为(0,9)或(0,﹣5).
,一次函数解析式为y=x+2;(3)点P的坐标为(0,9)或(0,﹣5).
【解析】
(1)利用![]() 直接写出A点坐标和B点坐标,再利用平分线分线段成比例定理计算出CD得到C点坐标;
直接写出A点坐标和B点坐标,再利用平分线分线段成比例定理计算出CD得到C点坐标;
(2)利用待定系数法求反比例函数解析式和一次函数解析式;
(3)设![]() ,利用三角形面积公式得到
,利用三角形面积公式得到![]() ,然后其出t得到点P的坐标.
,然后其出t得到点P的坐标.
解:(1)∵OA=OB=OD=2.
∴A点坐标为(﹣2,0),B点坐标为(0,2),
∵![]() ,
,
∴OB:CD=OA:AD,
∴CD=![]() =4,
=4,
∴C点坐标为(2,4),
(2)把C(2,4)代入y=![]() 得m=2×4=8,
得m=2×4=8,
∴反比例函数解析式为![]() ,
,
把A(﹣2,0),B(0,2)代入y=kx+b得![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=x+2;
(3)设P(0,t),
∵S△ACP=14,
而S△PBA+S△PBC=S△PAC,
∴![]() |t﹣2|×4=14,解得t=9或t=﹣5,
|t﹣2|×4=14,解得t=9或t=﹣5,
∴点P的坐标为(0,9)或(0,﹣5).


科目:初中数学 来源: 题型:
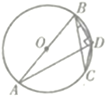
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,连接AD、BC、BD、DC,若BD = CD,∠DBC = 20°,则,∠ABC =_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,当点
,当点![]() 、
、![]() 、
、![]() 三点共线时,旋转角为
三点共线时,旋转角为![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,下面结论:①
,下面结论:①![]() 为等腰三角形;②
为等腰三角形;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 中,正确结论的个数是( )
中,正确结论的个数是( )
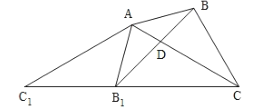
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小红玩一个游戏:一张卡片上标上数字0,另有n张质地都相同的卡片上标有数字1,2,3,…,n,将标有数字的一面朝下,小明从中任意抽取一张后放回洗匀,然后再取出一张;小红从中任意抽取一张后不放回,直接再抽取一张.
(1)n=3时,分别求小明抽出的两张卡片上的数积为0的概率与小红抽出的两张卡片上的数积为0的概率.(请用画树状图或列表的形式给出分析过程)
(2)小明抽出的两张卡片上的数积为0的概率是__________(用n表示);小红抽出的两张卡片上的数积为0的概率是__________(用n表示)
(3)若小红抽出的两张卡片上的数积为0的概率小于![]() ,则n的值至少是
,则n的值至少是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是正方形ABCD的边BC、CD的中点,连接AF、DE交于点P,过B作BG∥DE交AD于G,BG与AF交于点M.对于下列结论:①AF⊥DE;②G是AD的中点;③∠GBP=∠BPE;④S△AGM:S△DEC=1:4.正确的个数是( )
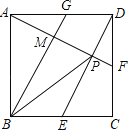
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.
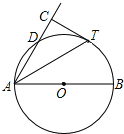
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,CT=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
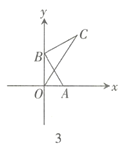
【题目】(1)问题发现
如图1,![]() 和
和![]() 均为等边三角形,直线
均为等边三角形,直线![]() 和直线
和直线![]() 交于点
交于点![]() .
.
填空:①![]() 的度数是 ;
的度数是 ;
②线段![]() ,
,![]() 之间的数量关系为 .
之间的数量关系为 .
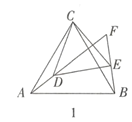
(2)类比探究
如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 和直线
和直线![]() 交于点
交于点![]() .请判断
.请判断![]() 的度数及线段
的度数及线段![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
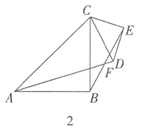
(3)解决问题
如图3,在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 为
为![]() 轴上任意一点,连接
轴上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,连接
,连接![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
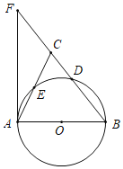
【题目】如图,AB是⊙O的直径,D是⊙O上一点,点E时![]() 的中点,过点A作⊙O的切线交BD的延长线于点F.连接AE并延长交BF于点C.
的中点,过点A作⊙O的切线交BD的延长线于点F.连接AE并延长交BF于点C.
(1)求证:AB=BC;
(2)如果AB=10.tan∠FAC=![]() ,求FC的长.
,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.

(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com