
| A. | 994 | B. | 995 | C. | 998 | D. | 999 |
分析 多位数1248624…是怎么来的?当第1个数字是1时,将第1位数字乘以2得2,将2写在第2位上,再将第2位数字2乘以2得4,将其写在第3位上,将第3位数字4乘以2得8,将8写在第4位上,将第4位数字8乘以2得16,将16的个位数字6写在第5位上,将第5位数字6乘以2得12,将12的个位数字2写在第6位上,再将第6位数字2乘以2得4,将其写在第7位上,以此类推.根据此方法可得到第一位是3的多位数后再求和.
解答 解:当第1位数字是3时,按如上操作得到一个多位数36 2486 2486 2486 2486 ….
仔细观察36 2486 2486 2486 2486 …中的规律,这个多位数前200位中前两个为36,接着出现2486 2486 2486…,所以36 2486 2486 2486 2486 …的前200位是36 2486 2486 2486…2486 2486 2486 24(因为198÷4=49余2,所以这个多位数开头两个36中间有49个2486,最后两个24),因此,这个多位数前200位的所有数字之和=(3+6)+(2+4+8+6)×49+(2+4)=9+980+6=995.
故选:B.
点评 本题是一个“数字游戏”而已,主要考查考生的阅读能力和观察能力,其解题的关键是:读懂题目,理解题意.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
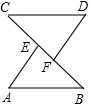 如图,已知EC=BF,AB∥CD,现有下列5个条件:①AE=DF;②∠B=∠C;③DF∥AE;④∠A=∠D;⑤AB=CD;从中选取一个条件,以保证△ABE≌△DCF,则可选择的有( )
如图,已知EC=BF,AB∥CD,现有下列5个条件:①AE=DF;②∠B=∠C;③DF∥AE;④∠A=∠D;⑤AB=CD;从中选取一个条件,以保证△ABE≌△DCF,则可选择的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -12与(-1)2 | B. | $\frac{{2}^{2}}{3}$与($\frac{2}{3}$)2 | C. | -|-2|与-(-2) | D. | (-3)3与-33 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com