
 ��ͼ����A��B������ֱ��ǣ�0��4������3��0������C���߶�AB���е㣬����P�ӵ�A��������AO������ÿ��1����λ���ٶ����յ�O�˶���ͬʱ����Q��O��������ÿ��2����λ���ٶ�����OB�����˶�����B������BA�������յ�A�˶�����CP��CQΪ�ڱ߹���ƽ���ı���PCQD�����P���˶�ʱ��Ϊt�룮
��ͼ����A��B������ֱ��ǣ�0��4������3��0������C���߶�AB���е㣬����P�ӵ�A��������AO������ÿ��1����λ���ٶ����յ�O�˶���ͬʱ����Q��O��������ÿ��2����λ���ٶ�����OB�����˶�����B������BA�������յ�A�˶�����CP��CQΪ�ڱ߹���ƽ���ı���PCQD�����P���˶�ʱ��Ϊt�룮���� ��1�������P���꣬�����������빫ʽ���㼴�ɣ�
��2����ͼ2�У�����PB��CD��K������ƽ���ı��ε����ʿ���֤������Q��B�غ�ʱ��CD��PA���ɴ˼��ɽ�����⣮
��3���辭��P��B��C����������ߵĽ���ʽΪy=ax2+bx+c��P��0��4-t����C��$\frac{3}{2}$��2����B��3��0������õ�$\left\{\begin{array}{l}{c=4-t}\\{\frac{9}{4}a+\frac{3}{2}b+c=2}\\{9a+3b+c=0}\end{array}\right.$���ɵ������ߵĽ���ʽΪy=-$\frac{2}{9}$tx2+��t-$\frac{4}{3}$��x+4-t���Ƴ������߶����������=$\frac{4����-\frac{2}{9}t����4-t��-��t-\frac{4}{3}��^{2}}{4����-\frac{2}{9}t��}$=$\frac{1}{8}t+\frac{2}{t}$+1=$\frac{1}{8}$��$\sqrt{t}$-$\sqrt{\frac{16}{t}}$��2+2���ɴ˼��ɽ�����⣮
��4���������������ۼ��ɢ���ͼ3�У����߶�PD���߶�OCû�н���ʱ���ص��������ı���PCKD����Ȼ����������������ͼ4�У����߶�PD���߶�OC�н���ʱ����OC��PD��K���ص��������ı��Ρ�PCK���۵���Q���߶�BC��ʱ����ͼ6�У��ص������ǡ�PCK���ܵ���Q���߶�AC��ʱ���ص��������ı���PCQK����ͼ���֪����Ȼ������������
��� �⣺��1����ͼ1�У�
��A��0��4����B��3��0����
��OA=4��OB=3��AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5��
�ߵ�C���߶�AB���е㣬
��OC=AC=BC=$\frac{5}{2}$��C��$\frac{3}{2}$��2����
��t=1��
��AP=1��P��0��3����
��PC=$\sqrt{{1}^{2}+��\frac{3}{2}��^{2}}$=$\frac{1}{2}$$\sqrt{13}$��
��2����ͼ2�У�����PB��CD��K��
��PC��DQ��PD��CQ��
���ı���PCQD��ƽ���ı��Σ�
��PK=KQ��
�൱Q��B�غ�ʱ����K�ĺ�����Ϊ$\frac{0+3}{2}$=$\frac{3}{2}$����C��$\frac{3}{2}$��2����
��CK��AP����CD��PA����ʱt=$\frac{3}{2}$s��
��3���辭��P��B��C����������ߵĽ���ʽΪy=ax2+bx+c��
��P��0��4-t����C��$\frac{3}{2}$��2����B��3��0������õ�$\left\{\begin{array}{l}{c=4-t}\\{\frac{9}{4}a+\frac{3}{2}b+c=2}\\{9a+3b+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{2}{9}t}\\{b=t-\frac{4}{3}}\\{c=4-t}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\frac{2}{9}$tx2+��t-$\frac{4}{3}$��x+4-t��
�������߶����������=$\frac{4����-\frac{2}{9}t����4-t��-��t-\frac{4}{3}��^{2}}{4����-\frac{2}{9}t��}$=$\frac{1}{8}t+\frac{2}{t}$+1=$\frac{1}{8}$��$\sqrt{t}$-$\sqrt{\frac{16}{t}}$��2+2��
�൱$\sqrt{t}$=$\sqrt{\frac{16}{t}}$ʱ�������߶�������������СֵΪ2��
��t=2ʱ�������߶�������������СֵΪ2��
��4������ͼ3�У����߶�PD���߶�OCû�н���ʱ���ص��������ı���PCKD����Ȼ������������
����ͼ4�У����߶�PD���߶�OC�н���ʱ����OC��PD��K���ص��������ı��Ρ�PCK��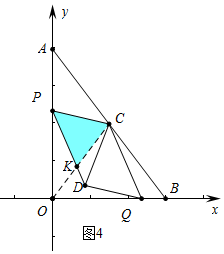
���˶�������ƽ���ı���PCQD�����Ϊs�������AOC���ص������Ϊs1��$\frac{{s}_{1}}{s}$��$\frac{1}{3}$��
�൱PK��2KDʱ��$\frac{{s}_{1}}{s}$��$\frac{1}{3}$��
����Q���B�غ�ʱ����ͼ5�У�
��PK��AC��
��$\frac{OP}{OA}$=$\frac{PK}{AC}$��
��$\frac{2.5}{4}$=$\frac{PK}{AC}$��
��PK=$\frac{5}{8}$AC=$\frac{5}{8}$BC=$\frac{5}{8}$PD��
��PK=$\frac{5}{3}$KD����ʱ��$\frac{{s}_{1}}{s}$��$\frac{1}{3}$������������
��ͼ4�У���P��0��4-t����C��$\frac{3}{2}$��2����Q��2t��0�������D����Ϊ��m��n������$\frac{\frac{3}{2}+m}{2}$=$\frac{2t}{2}$��$\frac{2+n}{2}$=$\frac{4-t+0}{2}$��
��m=2t-$\frac{3}{2}$��n=2-t��
��D��2t-$\frac{3}{2}$��2-t����
��ֱ��CQ�Ľ���ʽΪy=$\frac{4}{3-4t}$x+$\frac{8t}{4t-3}$��
ֱ��PD�Ľ���ʽΪy=$\frac{4}{3-4t}$x+4-t��
ֱ��OC�Ľ���ʽΪy=$\frac{4}{3}$x��
��$\left\{\begin{array}{l}{y=\frac{4}{3}x}\\{y=\frac{4}{3-4t}x+4-t}\end{array}\right.$���$\left\{\begin{array}{l}{x=\frac{3��t-4����3-4t��}{16t}}\\{y=\frac{��t-4����3-4t��}{4t}}\end{array}\right.$��
��k��$\frac{3��t-4����3-4t��}{16t}$��$\frac{��t-4����3-4t��}{4t}$����
��PK=2KDʱ��PK��PD=2��3��
��$\frac{3��t-4����3-4t��}{16t}$����2t-$\frac{3}{2}$��=2��3��
���t=$\frac{36}{25}$��
�൱$\frac{36}{25}$��t��$\frac{3}{2}$ʱ��$\frac{{s}_{1}}{s}$��$\frac{1}{3}$��
�۵���Q���߶�BC��ʱ����ͼ6�У��ص������ǡ�PCK��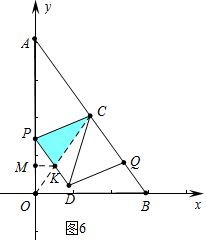
��KM��OP��M��
��OC=AC=CB��
���OCA=��CAO��
��PD��AB��
���KPO=��CAO=��KOP��
��PK=KO��
��PM=OM=$\frac{4-t}{2}$��
�ߡ�PMK�ס�AOB��
��$\frac{PK}{AB}$=$\frac{PM}{OA}$��
��$\frac{PK}{5}$=$\frac{\frac{4-t}{2}}{4}$��
��PK=$\frac{5}{8}$��4-t����
��PD=CQ=3+$\frac{5}{2}$-2t=$\frac{11}{2}$-2t��
��PK��PD=2��3ʱ��
$\frac{5}{8}$��4-t������$\frac{11}{2}$-2t��=2��3��
���t=$\frac{28}{17}$��
�൱$\frac{3}{2}$��t��$\frac{28}{17}$ʱ��$\frac{{s}_{1}}{s}$��$\frac{1}{3}$��
�ܵ���Q���߶�AC��ʱ���ص��������ı���PCQK����ͼ���֪����Ȼ������������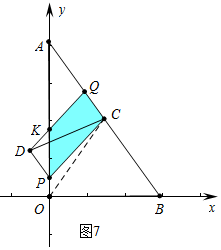
������������$\frac{36}{25}$��t��$\frac{28}{17}$ʱ��$\frac{{s}_{1}}{s}$��$\frac{1}{3}$��
���� ���⿼����κ����ۺ��⡢һ�κ�����Ӧ�á������������⡢���������ε��ж������ʡ�ƽ���ı��ε����ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬ע�ⲻ��©�⣬ѧ�������䷽��ȷ��������ֵ���⣬�����п�ѹ���⣮


 Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д� �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ�������ϣ��ش����⣺
�Ķ�������ϣ��ش����⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ʽ-2��R2�Ĵ�����3��ϵ����-2 | |
| B�� | ����ʽ-$\frac{3{x}^{2}{y}^{2}}{5}$��ϵ����3��������4 | |
| C�� | $\frac{a+b}{3}$���Ƕ���ʽ | |
| D�� | ����ʽ3x2-5x2y2-6y4-2���Ĵ�����ʽ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5 | B�� | -10 | C�� | -5�� | D�� | -10�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5cm��9cm��12cm | B�� | 7cm��12cm��13cm | C�� | 30cm��40cm��50cm | D�� | 3cm��4cm��6cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | һ | �� | �� | �� | �� | �� | �� |
| ���� | -5 | +2 | +8 | -6 | +10 | +3 | -4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com