Question

4．如图1，矩形ABCD中，P是AB边上的一点（不与A，B重合），PE平分∠APC交射线AD于E，过E作EM⊥PE交直线CP于M，交直线CD于N．
（1）求证：CM=CN；
（2）若AB：BC=4：3，
①当$\frac{AP}{PB}$=$\frac{9}{55}$时，E恰好是AD的中点；
②如图2，当△PEM与△PBC相似时，求$\frac{EN}{EM}$的值．

Answer 1

分析 （1）由矩形的性质得出∠A=∠ADC=90°，AB=CD，AD=BC，由平行线的性质、互余两角关系、对顶角相等以及角平分线证出∠CMN=∠N，即可得出结论；
（2）①由题意得出M、N、C三点重合，由ASA证明△APE≌△DFE，得出AP=DF，PE=FE，由线段垂直平分线的性质证出AP+CD=PC，设AD=3，AB=4，过P作PF⊥CD于F，设AP=DE=x，则PB=CF=4-x，PC=4+x，PF=3，由勾股定理得出方程，解方程即可；
②分两种情况：1．若△PEM∽△CCBP，则∠EPM=∠BCP，得出PE∥BC，不成立；
2．若△PEM∽△PBC，则∠APB=∠EPM=∠BPC=60°，设AB=4a，BC=AD=3a，则PB=$\sqrt{3}$a，AP=（4-$\sqrt{3}$）a，AE=（4$\sqrt{3}$-3）a，设PE与CD交于点F，证出△PEM∽△FEN，由相似三角形的性质和平行线分线段成比例定理得出$\frac{EN}{EM}=\frac{EF}{EP}$=$\frac{DE}{AE}$，即可得出结果．

解答 （1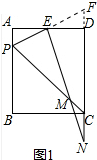）证明：延长PE交CD的延长线于F，如图1所示：
∵四边形ABCD是矩形，
∴AB∥CD，∠A=∠ADC=∠EDF═90°，AB=CD，AD=BC，
∴∠APE+∠AEP=90°，
∴∠F=∠APE，
∵EM⊥EN，
∴∠PEN=∠FEN=90°，
∴∠CPE+∠PME=90°，∠F+∠N=90°，
∵PE平分∠APC，
∴∠APE=∠MPE，
又∵∠PME=∠CMN，
∴∠CMN=∠N，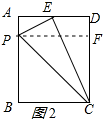
∴CM=CN；
（2）解：①若E是AD的中点，则M、N、C三点重合，
∵E为AD的中点，
∴AE=DE，
在△APE和△DFE中，$\left\{\begin{array}{l}{∠A=∠EDF}&{\;}\\{AE=DE}&{\;}\\{∠AEP=∠DEF}&{\;}\end{array}\right.$，
∴△APE≌△DFE（ASA），
∴AP=DF，PE=FE，
∵EM⊥EN，
∴PC=FC，
∵FC=CD+DF，
∴AP+CD=PC，
设AD=3a，AB=4a，
过P作PF⊥CD于F，如图2所示：
设AP=DE=x，则PB=CF=4-x，PC=4+x，PF=3，
由勾股定理得：（4-x）²+3²=（4+x）²，
解得：x=$\frac{9}{16}$a，4-x=$\frac{55}{16}$a，
∴$\frac{AP}{PB}=\frac{9}{55}$；
②分两种情况：
1．若△PEM∽△CCBP，则∠EPM=∠BCP，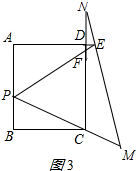
∴PE∥BC，不成立；
2．若△PEM∽△PBC，则∠APB=∠EPM=∠BPC=60°，
设AB=4a，BC=AD=3a，
则PB=$\sqrt{3}$a，AP=（4-$\sqrt{3}$）a，AE=（4$\sqrt{3}$-3）a，
设PE与CD交于点F，如图3所示：
∵AB∥CD，
∴∠EFN=∠BFC=∠APE=60°，
∴∠N=∠M=90°-60°=30°，
∵EM⊥PE，
∴∠NEF=∠PEM=90°，
∴△PEM∽△FEN，
∴$\frac{EN}{EM}=\frac{EF}{EP}$，
∵AB∥CD，
∴$\frac{EF}{EP}=\frac{DE}{AE}$，
∴$\frac{EN}{EM}=\frac{EF}{EP}$=$\frac{DE}{AE}$=$\frac{4\sqrt{3}-6}{4\sqrt{3}-3}$=$\frac{10-4\sqrt{3}}{13}$．

点评 本题考查了矩形的性质、等腰三角形的判定、勾股定理、线段垂直平分线的性质、全等三角形的判定与性质、相似三角形的判定与性质等知识；本题综合性强，有一定难度，熟练掌握矩形的性质和等腰三角形的判定，证明三角形相似是解决问题的关键．