
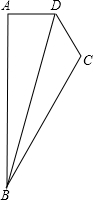
 如图,四边形ABCD中,∠DAB=90°,AD=CD,∠BCD=∠CDA=120°,则$\frac{{S}_{△ABD}}{{S}_{△BDC}}$=$\frac{4}{3}$.
如图,四边形ABCD中,∠DAB=90°,AD=CD,∠BCD=∠CDA=120°,则$\frac{{S}_{△ABD}}{{S}_{△BDC}}$=$\frac{4}{3}$. 分析 延长AD、BC相交于点E,求出∠CDE=∠DCE=60°,从而判断出△CDE是等边三角形,过点D作DF⊥CE于F,设AD=CD=x,然后求出AE、DF,再求出AB、BC,最后根据三角形的面积公式列式求解即可.
解答 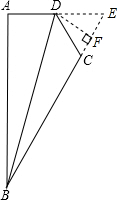 解:如图,延长AD、BC相交于点E,
解:如图,延长AD、BC相交于点E,
∵∠BCD=∠CDA=120°,
∴∠CDE=∠DCE=60°,
∴△CDE是等边三角形,
∴CD=DE=CE,∠E=60°,
过点D作DF⊥CE于F,设AD=CD=x,
则AE=AD+DE=x+x=2x,
DF=$\frac{\sqrt{3}}{2}$CD=$\frac{\sqrt{3}}{2}$x,
∵∠E=60°,∠DAB=90°,
∴AB=$\sqrt{3}$AE=2$\sqrt{3}$x,
BE=2AE=2•2x=4x,
∴BC=BE-CE=4x-x=3x,
∴S△ABD=$\frac{1}{2}$AB•AD=$\frac{1}{2}$•2$\sqrt{3}$x•x=$\sqrt{3}$x2,
S△BDC=$\frac{1}{2}$BC•DF=$\frac{1}{2}$•3x•$\frac{\sqrt{3}}{2}$x=$\frac{3\sqrt{3}}{4}$x2,
所以,$\frac{{S}_{△ABD}}{{S}_{△BDC}}$=$\frac{\sqrt{3}{x}^{2}}{\frac{3}{4}\sqrt{3}{x}^{2}}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了等边三角形的判定与性质,解直角三角形,作辅助线构造出等边三角形以及有一个角是60°的直角三角形是解题的关键,也是本题的难点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:填空题
下面的框图表示解方程3x-7(x-1)=3-2(x+3)的流程,其中A代表的步骤是_________,步骤A对方程进行变形的依据是________________。

查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:单选题
甲、乙两人同时开始采摘樱桃,甲平均每小时采摘8公斤樱桃,乙平均每小时采摘7公斤樱桃。采摘同时结束后,甲从他采摘的樱桃中取出1公斤给了乙,这时两人的樱桃一样多。他们采摘樱桃用了多长时间?设他们采摘了x小时,则下面所列方程中正确的是( )
A. 8x-1=7x+1 B. 8x-1=7x C. 8x+l=7x D. 8x+l=7x-1
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间(秒) 路程(米) | 从比赛开始到 匀速跑前 | 从比赛开始到 匀速跑完100秒 | 从比赛开始到 匀速跑完200秒 |
| 小明 | 1600 | 1600+100a | 1600+200a |
| 小刚 | 1450 | 1450+100b | 1450+200b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,圆O的半径为2$\sqrt{2}$,AB、AC是圆O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与AC相切的圆,那么这个圆的半径是多少?它与AB又怎样的位置关系?为什么?
如图,圆O的半径为2$\sqrt{2}$,AB、AC是圆O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与AC相切的圆,那么这个圆的半径是多少?它与AB又怎样的位置关系?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
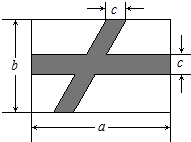 如图所示,在公园长方形空地上,要修两条路(图中的阴影所示),按照图中标的数据,计算图中空白部分的面积为( )
如图所示,在公园长方形空地上,要修两条路(图中的阴影所示),按照图中标的数据,计算图中空白部分的面积为( )| A. | ab-bc-ac+c2 | B. | bc-ab+ac | C. | b2-bc+a2-ab | D. | a2+ab+bc-ac |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com