
【题目】如图,射线![]() 上有三点
上有三点![]() 、
、![]() 、
、![]() ,满足
,满足![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度匀速运动,点
的速度匀速运动,点![]() 从点
从点![]() 出发在线段
出发在线段![]() 上向点
上向点![]() 匀速运动,两点同时出发,当点
匀速运动,两点同时出发,当点![]() 运动到点
运动到点![]() 时,点
时,点![]() 、
、![]() 停止运动.
停止运动.


(1)若点![]() 运动速度为
运动速度为![]() ,经过多长时间
,经过多长时间![]() 、
、![]() 两点相遇?
两点相遇?
(2)当![]() 时,点
时,点![]() 运动到的位置恰好是线段
运动到的位置恰好是线段![]() 的中点,求点
的中点,求点![]() 的运动速度;
的运动速度;
(3)设运动时间为![]() ,当点
,当点![]() 运动到线段
运动到线段![]() 上时,分别取
上时,分别取![]() 和
和![]() 的中点
的中点![]() 、
、![]() ,则
,则![]() ____________
____________![]() .
.
【答案】(1)经过![]() ,
,![]() 、
、![]() 两点相遇(2)答案不唯一,具体见解析(3)
两点相遇(2)答案不唯一,具体见解析(3)![]()
【解析】
(1)设经过t秒时间P、Q两点相遇,根据OP+CQ=OA+AB+AC列出方程即可解决问题;
(2)分两种情形求解即可;
(3)用t表示AP、EF的长,代入化简即可解决问题;
(1)设运动时间为![]() ,则
,则![]() ,
,![]() ;所以经过
;所以经过![]() ,
,![]() 、
、![]() 两点相遇
两点相遇
(2)当点![]() 在线段
在线段![]() 上时,如下图,
上时,如下图,
AP+PB=60,
∴AP=40,OP=50,
∴P用时50s,
∵Q是OB中点,
∴CQ=50,
点![]() 的运动速度为
的运动速度为![]()
![]() ;
;

当点![]() 在线段
在线段![]() 的延长线上时,如下图,
的延长线上时,如下图,
AP=2PB,
∴AP=120,OP=140,
∴P用时140s,
∵Q是OB中点,
∴CQ=50,
点![]() 的运动速度为
的运动速度为![]()
![]() ;
;

(3)如下图,

由题可知,OC=90,
AP=x-20,
EF=OF-OE=OF-![]() OP=50-
OP=50-![]() x,
x,
∴![]() 90-(x-20)-2(50-
90-(x-20)-2(50-![]() x)=10
x)=10


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图7所示,点![]() 、
、![]() 、
、![]() 在
在![]() 轴上,且
轴上,且![]() ,分别过点
,分别过点![]() 、
、![]() 、
、![]() 作
作![]() 轴的平行线,与反比例函数
轴的平行线,与反比例函数![]() 的图象分别交于点
的图象分别交于点![]() 、
、![]() 、
、![]() ,分别过点
,分别过点![]()
![]()
![]() 作
作![]() 轴的平行线,分别与
轴的平行线,分别与![]() 轴交于点
轴交于点![]()
![]()
![]() ,连接
,连接![]()
![]()
![]() ,那么图中阴影部分的面积之和为___________.
,那么图中阴影部分的面积之和为___________.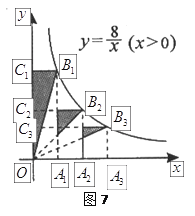
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由6相同的小正方体组合成的简单几何体.
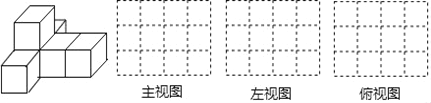
(1)请在方格纸中分别画出几何体的主视图、左视图和俯视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
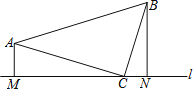
【题目】如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作直线![]() 的垂线,垂足分别为M、N.
的垂线,垂足分别为M、N.
(1)求证:△AMC≌△CNB;
(2)若AM=3,BN=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
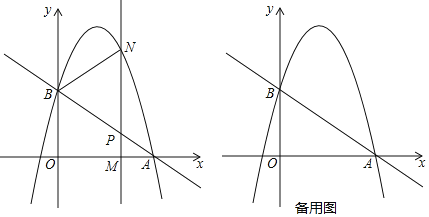
【题目】如图,抛物线![]() 过点
过点![]() ,
, ![]() .
. ![]() 为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)如果以B,P,N为顶点的三角形与![]() 相似,求点M的坐标.
相似,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三点A、B、C,请根据图回答下列问题:
![]()
(1)若将点B向左平移3个单位后,则A、B、C这三个点所表示的数谁最小?是多少?
(2)若将点A向右平移4个单位后,则A、B、C这三个点所表示的数谁最大?最大的数比最小的数大多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一张平行四边形纸片ABCD,要求利用所学知识作出一个菱形,甲、乙两位同学的作法分别如下:
甲:连接AC,作AC的中垂线交AD、BC于E、F,则四边形AFCE是菱形. | 乙:分别作 |
对于甲、乙两人的作法,可判断( )

A.甲正确,乙错误B.甲错误,乙正确
C.甲、乙均正确D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有相同的三个小球,其上面分别标注
数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回
袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com