
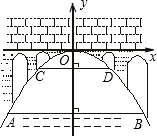
 如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m.
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m.分析 (1)根据函数图象可以设出函数解析式,然后根据题目中的数据可以求得此抛物线的解析式;
(2)根据题意可以求得货车按原速到达搭桥的时间,也可以求得安全通过此桥用的时间,然后进行比较即可解答此题;
(3)根据题意可以求得此船到达此桥用的时间,也可以求得升到最大水位用的时间,然后进行比较即可解答此题.
解答 解:(1)设所求抛物线的解析式为:y=ax2,点D的坐标为(5,b),点B(10,b-15),
b=a×52,b-15=a×102,
解得,a=$-\frac{1}{5}$,b=-5,
即抛物线的解析式为y=$-\frac{1}{5}{x}^{2}$;
(2)货车原速行驶到达搭桥所需时间为:480÷40-1=11小时,
∵点D(5,-5),
∴到搭桥禁止通行还有:(5-3)÷0.25=8小时,
∵11>8,
∴货车按原来速度行驶,不能安全通过此桥,
∵(480-40)÷8=55,
∴若要安全通过此桥,则车速应超过55千米/时;
(3)当x=2时,y=$-\frac{1}{5}×{2}^{2}=-0.8$,
∵D(5,-5),
∴5-0.8-3.5=0.7,
即船要顺利通过此桥,水位最多上升0.7米,所需时间为:0.7÷0.25=2.8小时,
∵40÷20=2小时,2.8>2,
∴此船可以安全通过此桥.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,明确图象上点的坐标代表的实际意义.


科目:初中数学 来源: 题型:选择题
| A. | x$<\frac{3}{2}$ | B. | x$<-\frac{3}{2}$ | C. | x$>\frac{3}{2}$ | D. | x$>-\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
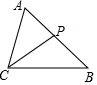 如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )
如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com