练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列事件中，必然事件是

    A. 抛掷一枚硬币，正面朝上

    B. 打开电视，正在播放广告

    C. 体育课上，小刚跑完1000米所用时间为1分钟

    D. 袋中只有4个球，且都是红球，任意摸出一球是红球


    D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，点P（﹣1，1）在双曲线上，过点P的直线l1与坐标轴分别交于A、B两点，且tan∠BAO=1．点M是该双曲线在第四象限上的一点，过点M的直线l2与双曲线只有一个公共点，并与坐标轴分别交于点C、点D．则四边形ABCD的面积最小值为（　　）

    　

    A．

    10

    B．

    8

    C．

    6

    D．

    不确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在矩形ABCD中，AB=4，BC=3，点O为对角线BD的中点，点P从点A出发，沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动，当点P与点A不重合时，过点P作PQ⊥AB于点Q，以PQ为边向右作正方形PQMN，设正方形PQMN与△ABD重叠部分图形的面积为S（平方单位），点P运动的时间为t（秒）．

    （1）求点N落在BD上时t的值；

    （2）直接写出点O在正方形PQMN内部时t的取值范围；

    （3）当点P在折线AD﹣DO上运动时，求S与t之间的函数关系式；

    （4）直接写出直线DN平分△BCD面积时t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：（x+1）（x﹣1）﹣x（x﹣1），其中x=．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    阅读材料：如图1，在△AOB中，∠O=90°，OA=OB，点P在AB边上，PE⊥OA于点E，PF⊥OB于点F，则PE+PF=OA．（此结论不必证明，可直接应用）

    （1）【理解与应用】

    如图2，正方形ABCD的边长为2，对角线AC，BD相交于点O，点P在AB边上，PE⊥OA于点E，PF⊥OB于点F，则PE+PF的值为　　．

    （2）【类比与推理】

    如图3，矩形ABCD的对角线AC，BD相交于点O，AB=4，AD=3，点P在AB边上，PE∥OB交AC于点E，PF∥OA交BD于点F，求PE+PF的值；

    （3）【拓展与延伸】

    如图4，⊙O的半径为4，A，B，C，D是⊙O上的四点，过点C，D的切线CH，DG相交于点M，点P在弦AB上，PE∥BC交AC于点E，PF∥AD于点F，当∠ADG=∠BCH=30°时，PE+PF是否为定值？若是，请求出这个定值；若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线a∥b，将三角尺的直角顶点放在直线b上，

    ∠1=35°，则∠2= .


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，A、B两点分别在x轴和y轴上，

    OA=1，OB=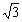，连接AB，过AB中点C1分别作x轴和y轴的

    垂线，垂足分别是点A1、B1，连接A1B1，再过A1B1中点C2作x

    轴和y轴的垂线，照此规律依次作下去，则点Cn的坐标为             .

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    化简 的结果是

     A．   　　       B．   　　　     C．  　　　     D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：a（a﹣3b）+（a+b）2﹣a（a﹣b），其中a=1，b=﹣．

    查看答案和解析>>

    同步练习册答案