
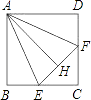
【题目】如图,在正方形ABCD中,点E、F分别在BC、CD上移动,但A到EF的距离AH始终保持与AB长相等,问在E、F移动过程中: 
(1)∠EAF的大小是否有变化?请说明理由.
(2)△ECF的周长是否有变化?请说明理由.
【答案】
(1)解:∠EAF的大小没有变化.理由如下:
根据题意,知
AB=AH,∠B=90°,
又∵AH⊥EF,
∴∠AHE=90°,
∵AE=AE,
∴Rt△BAE≌Rt△HAE(HL),
∴∠BAE=∠HAE,
同理,△HAF≌△DAF,
∴∠HAF=∠DAF,
∴∠EAF=∠EAH+∠FAH= ![]() ∠BAH+
∠BAH+ ![]() ∠HAD=
∠HAD= ![]() (∠BAH+∠HAD)=
(∠BAH+∠HAD)= ![]() ∠BAD,
∠BAD,
又∵∠BAD=90°,
∴∠EAF=45°,
∴∠EAF的大小没有变化.
(2)解:△ECF的周长没有变化.理由如下:
∵由(1)知,Rt△BAE≌Rt△HAE,△HAF≌△DAF,
∴BE=HE,HF=DF,
∴C△EFC=EF+EC+FC=EB+DF+EC+FC=2BC,
∴△ECF的周长没有变化.
【解析】(1)根据题意,求证△BAE≌△HAE,△HAF≌△DAF,然后根据全等三角形的性质求∠EAF= ![]() ∠BAD.(2)根据(1)的求证结果,用等量代换来计算△ECF的周长,如果结果是定量,就说明△ECF的周长没有变化,反之,△ECF的周长有变化.
∠BAD.(2)根据(1)的求证结果,用等量代换来计算△ECF的周长,如果结果是定量,就说明△ECF的周长没有变化,反之,△ECF的周长有变化.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示﹣ ![]() ,设点B所表示的数为m.
,设点B所表示的数为m. ![]()
(1)求m的值;
(2)求|m﹣1|+(m+6)0的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面相同的纸牌A、B、C、D其正面分别画有正三角形、圆、平行四边形、正五边形,某同学把这四张牌背面向上洗匀后摸出一张,放回洗匀再摸出一张. 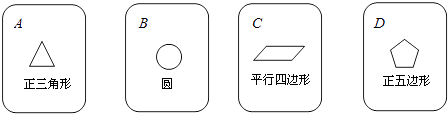
(1)请用树状图或表格表示出摸出的两张牌所有可能的结果;
(2)求摸出两张牌的牌面图形都是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:

(1)他们的对话内容,求小明和爸爸的骑行速度,
(2)一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸相距50m?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG; (2)OG= ![]() BC; ( 3)OGE是等边三角形; ( 4)SAOE=
BC; ( 3)OGE是等边三角形; ( 4)SAOE= ![]() S矩形ABCD
S矩形ABCD
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图,在Rt△ABC中,∠ACB=90°∠BAC=30°.
动手操作:(1)若以直角边AC所在的直线为对称轴.将Rt△ABC作轴对称变换,请你在原图上作出它的对称图形:
观察发现:(2)Rt△ABC和它的对称图形组成了什么图形?你最准确的判断是 .
合作交流:(3)根据上面的图形,请你猜想直角边BC与斜边AB的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com