
 小明发现:若设∠BAC=θ(0°<θ<90°).把小棒依次摆放在两射线AB、AC之间,并使小棒两端分别落在两射线上,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.若只能摆放5根小棒,则θ的范围是( )
小明发现:若设∠BAC=θ(0°<θ<90°).把小棒依次摆放在两射线AB、AC之间,并使小棒两端分别落在两射线上,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.若只能摆放5根小棒,则θ的范围是( )| A. | 10<θ<15 | B. | 15<θ≤20 | C. | 15≤θ<18 | D. | 20≤θ≤30 |
科目:初中数学 来源: 题型:填空题
 将两块全等的三角板如图放置,点O为AB中点,AB=A′B′=10,BC=B′C′=6,现将三角板A′B′C′绕点O旋转,B′C′、A′B′与边AC分别交于点M、N,当CM=$\frac{25}{8}$或$\frac{7}{4}$时,△OMN与△BCO相似.
将两块全等的三角板如图放置,点O为AB中点,AB=A′B′=10,BC=B′C′=6,现将三角板A′B′C′绕点O旋转,B′C′、A′B′与边AC分别交于点M、N,当CM=$\frac{25}{8}$或$\frac{7}{4}$时,△OMN与△BCO相似.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{sin20°}$ | B. | $\frac{5}{cos20°}$ | C. | $\frac{5}{tan20°}$ | D. | 5tan20° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0<a<$\frac{1}{4}$ | B. | a>$\frac{1}{4}$ | C. | a<0 | D. | 不存在 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
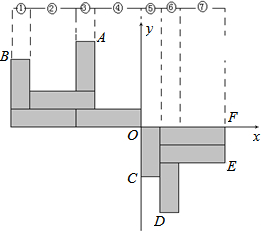 用如图大小形状完全相同的长方形纸片在直角坐标系中摆成以下图案,已知A(-2,6).
用如图大小形状完全相同的长方形纸片在直角坐标系中摆成以下图案,已知A(-2,6).| 范围顺序号 | m的范围 | n对应的范围 |
| 1 | -2≤m≤0 | 0$≤n≤\frac{4}{3}$ |
| 2 | -$\frac{10}{3}$≤m<-2 | 0≤n≤6 |
| 3 | -$\frac{16}{3}$≤m<-$\frac{10}{3}$ | 0≤n≤$\frac{8}{3}$ |
| 4 | -$\frac{20}{3}$≤m<-$\frac{16}{3}$ | 0$≤n≤\frac{14}{3}$ |
| 5 | 0<m$≤\frac{4}{3}$ | -$\frac{10}{3}$≤n≤0 |
| 6 | $\frac{4}{3}$<m≤$\frac{8}{3}$ | -6≤n≤0 |
| 7 | $\frac{8}{3}$<m≤$\frac{14}{3}$ | 0≤n≤-$\frac{8}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com