
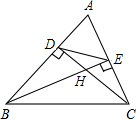
 如图,BE,CD分别是锐角△ABC的高,BE与CD相交于H,连接DE.分别找出与△HDE,△ADE相似的三角形,并说明理由.
如图,BE,CD分别是锐角△ABC的高,BE与CD相交于H,连接DE.分别找出与△HDE,△ADE相似的三角形,并说明理由. 分析 由已知条件易证△EHC∽△DHB,进而可得HE:HD=HC:BH,又因为∠DHE=∠BHC,所以可证明△HDE∽△HBC;由相似三角形的判定方法易证△ADC∽△AEB,所以AD:AE=AC:AB.又∠A=∠A,所以可证明△AED∽△ABC.
解答 解:△HDE∽△HBC,△ADE∽△ACB,
理由如下:
∵BE,CD分别是锐角△ABC的高,
∴∠HEC=∠HDB=90°,
∵∠DHB=∠HEC,
∴△EHC∽△DHB,
∴HE:HD=HC:BH,
又∵∠DHE=∠BHC,
∴△HDE∽△HBC;
∵CD、BE分别是锐角△ABC中AB、AC边上的高线,
∴∠ADC=∠AEB=90°,
又∵∠A=∠A,
∴△ADC∽△AEB,
AD:AE=AC:AB.
又∵∠A=∠A,
∴△AED∽△ABC.
点评 本题考查了相似三角形的判定.
(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
(2)三边法:三组对应边的比相等的两个三角形相似;
(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
(4)两角法:有两组角对应相等的两个三角形相似.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.
如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com