
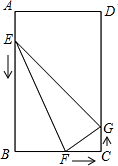
 如图,在矩形ABCD中,AB=12cm,BC=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2).
如图,在矩形ABCD中,AB=12cm,BC=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2).分析 (1)用t分别表示出AE,BE,BF,FC,CG,DG,根据矩形、三角形和梯形的面积公式列出方程,解方程得到答案;
(2)分△EBF∽△FCG和△EBF∽△GCF两种情况根据相似三角形的性质列出关系式求出t值;
(3)分∠EFG=90°和∠EGF=90°两种情况,根据勾股定理列出方程,解方程即可.
解答 解:(1)由题意得,AE=2t,BE=12-2t,BF=4t,FC=8-4t,CG=2t,DG=12-2t,
12×8-$\frac{1}{2}$×(12-2t)×4t-$\frac{1}{2}$×(8-4t)×2t-$\frac{1}{2}$×12×8=12×8×$\frac{1}{6}$,
整理得,t2-4t+4=0,
解得,t1=t2=2,
答:2秒后,S的值是矩形ABCD面积的$\frac{1}{6}$;
(2)当△EBF∽△FCG时,
$\frac{BE}{FC}$=$\frac{BF}{CG}$,即$\frac{12-2t}{8-4t}$=$\frac{4t}{2t}$,
解得,t=$\frac{2}{3}$,
当△EBF∽△GCF时,
$\frac{EB}{FC}$=$\frac{BF}{FC}$,即$\frac{12-2t}{2t}$=$\frac{4t}{8-4t}$,
解得,t=$\frac{3}{2}$,
∴当t=$\frac{2}{3}$或$\frac{3}{2}$时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似;
(3)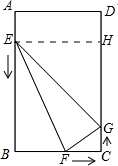 作EH∥AD交DC于H,
作EH∥AD交DC于H,
则DH=2t,HG=12-4t,
由勾股定理得,EG2=64+(12-4t)2=16t2-96t+208,
EF2=(12-2t)2+(4t)2=20t2-48t+144,
GF2=(8-4t)2+(2t)2=20t2-64t+64,
当∠EFG=90°时,20t2-48t+144+20t2-64t+64=16t2-96t+208,
解得t1=0(舍去),t2=$\frac{2}{3}$,
当∠EGF=90°时,20t2-48t+144=20t2-64t+64+16t2-96t+208,
解得t1=$\frac{7-\sqrt{17}}{2}$,t2=$\frac{7+\sqrt{17}}{2}$(舍去).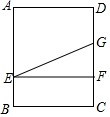 当点F在CD边上时,
当点F在CD边上时,
∠EFG=90°时,BE=CF,即12-2t=4t-8,
解得,t=$\frac{10}{3}$,
∠EGF=90°时,BE=CF,即2t=12-2t,
解得,t=3,
∴当t=$\frac{2}{3}$或$\frac{7-\sqrt{17}}{2}$或t=$\frac{10}{3}$或t=3时,△EFG是直角三角形,
故答案为:$\frac{2}{3}$或$\frac{7-\sqrt{17}}{2}$或t=$\frac{10}{3}$或t=3.
点评 本题考查的是矩形的性质、相似三角形的性质和一元二次方程的应用,掌握相关的性质和定理、正确解出方程是解题的关键.注意分情况讨论思想的正确运用.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有一条长7.2米的木料,做成如图所示的“目”字形的窗框,问窗的高和宽各取多少米时,这个窗的面积最大?(不考虑木料加工时损耗和中间木框所占的面积)
有一条长7.2米的木料,做成如图所示的“目”字形的窗框,问窗的高和宽各取多少米时,这个窗的面积最大?(不考虑木料加工时损耗和中间木框所占的面积)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
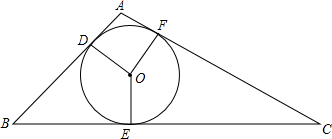 如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.
如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com