
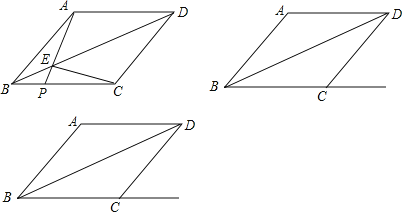
【题目】如图,菱形ABCD中,AB=10,连接BD,点P是射线BC上一点(不与点B重合),AP与对角线BD交于点E,连接EC.
(1)求证:AE=CE;
(2)若sin∠ABD=![]() ,当点P在线段BC上时,若BP=4,求△PEC的面积;
,当点P在线段BC上时,若BP=4,求△PEC的面积;
(3)若∠ABC=45°,当点P在线段BC的延长线上时,请直接写出△PEC是等腰三角形时BP的长.
【答案】(1)详见解析;(2)![]() ;(3)△PEC是等腰三角形时BP的长为10
;(3)△PEC是等腰三角形时BP的长为10![]() 或
或![]() .
.
【解析】
(1)由菱形的性质得出∠ABE=∠CBE,AB=BC,由SAS证得△ABE≌△CBE,即可得出结论;
(2)连接AC,交BD于O,证明△BEP∽△DEA,![]() ,则
,则![]() ,求出OA=2
,求出OA=2![]() ,
,![]() ,BD=8
,BD=8![]() ,
,![]() ,
,![]() ,S△DEA
,S△DEA![]() ,S△ABE=
,S△ABE=![]() S△BEC,S△BEP=
S△BEC,S△BEP=![]() ,即可得出答案;
,即可得出答案;
(3) ①当CE=CP时,得出△PEC是等腰直角三角形,过点E作EF∥AB交BC于F,证出EF=BF,推出![]() CF+CF=BC=10,求出CF的长,即可得出答案;
CF+CF=BC=10,求出CF的长,即可得出答案;
②当CE=CP时,求得∠CPE=30°,∠BAE=∠BCE=105°,过点A作AN⊥BP于N,则△ABN是等腰直角三角形,得出AN=BN=![]() AB=5
AB=5![]() ,求出PN=5
,求出PN=5![]() ,即可得出答案.
,即可得出答案.
(1)∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=BC,
在△ABE和△CBE中, ,
,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)连接AC,交BD于O,如图1所示:
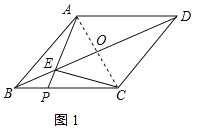
∵四边形ABCD是菱形,
∴AD∥BC,AD=AB=10,∠AOB=90°,OB=OD,OA=OC,
∴△BEP∽△DEA,
∴![]() ,
,
∴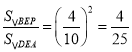 ,
,
∵sin∠ABD=![]() ,
,
∴OA=2![]() ,
,
![]() ,
,
∴BD=2OB=8![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴S△DEA=![]() OADE=
OADE=![]() ×2
×2![]() ×
×![]() ,
,
S△ABE=![]() OABE=
OABE=![]() ×2
×2![]() ×
×![]() S△BEC,
S△BEC,
∴S△BEP=![]() S△DEA=
S△DEA=![]() ×
×![]() =
=![]() ,
,
∴S△PEC=S△BEC﹣S△BEP=![]() =
=![]() ;
;
(3)①当CE=CP时,
∴∠CPE=∠CEP,
由(1)得:△ABE≌△CBE,
∴∠BAE=∠BCE,
∴∠BAE=∠BCE=∠CPE+∠CEP=2∠CPE,
∵∠ABC+∠BAE+∠CPE=180°,∠ABC=45°,
∴45°+2∠CPE+∠CPE=180°,
解得:∠CPE=45°,∠BAE=∠BCE=90°,
∴∠ECP=90°,
∴△PEC是等腰直角三角形,
过点E作EF∥AB交BC于F,如图所示:
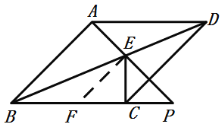
∴∠EFP=∠ABC=45°,∠FEP=∠BAP=90°,∠BEF=∠ABE=∠EBC,
∴∠FEC=∠FEP-∠CEP=90°-45°=45°,EF=BF,
则CE=CP=CF,EF=![]() CF,
CF,
∴![]() CF+CF=BC=10,
CF+CF=BC=10,
∴CF=![]() ,
,
∴BP=BC+CP=BC+CF=10+![]() =10
=10![]() ;
;
②当CE=CP时,
∴∠PCE=∠CEP,
由(1)得:△ABE≌△CBE,
∴∠AEB=∠CEB,
∴∠BAE=∠BCE=∠CPE+∠CEP=∠CPE+![]() ,
,
∵∠ABC+∠BAE+∠CPE=180°,∠ABC=45°,
∴45°+∠CPE+![]() +∠CPE=180°,
+∠CPE=180°,
解得:∠CPE=30°,∠BAE=∠BCE=105°,
过点A作AN⊥BP于N,如图3所示:
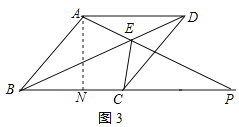
∵∠ABC=45°,
则△ABN是等腰直角三角形,
∴AN=BN=![]() AB=5
AB=5![]() ,
,
∵∠APB=30°,
∴tan30°=![]() ,即
,即![]() ,
,
∴PN=5![]() ,
,
∴BP=BN+PN=5![]() +5
+5![]() ,
,
综上所述,△PEC是等腰三角形时BP的长为10![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
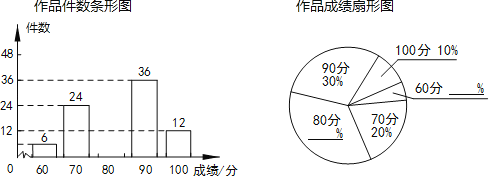
【题目】3月5日是学雷锋日,某校组织了以“向雷锋同志学习”为主题的小报制作比赛,评分结果只有60,70,80,90,100五种.现从中随机抽取部分作品,对其份数及成绩进行整理,制成如下两幅不完整的统计图.根据以下信息,解答下列问题:
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共1200份,请估计该校学生比赛成绩达到90分以上(含90分)的作品有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
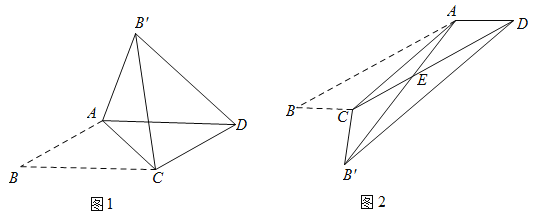
【题目】我们知道平行四边形有很多性质.
现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
(发现与证明)![]() ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.
ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.
结论1:B′D∥AC;
结论2:△AB′C与![]() ABCD重叠部分的图形是等腰三角形.
ABCD重叠部分的图形是等腰三角形.
……
请利用图1证明结论1或结论2(只需证明一个结论).
(应用与探究)在![]() ABCD中,已知∠B=30°,将△ABC沿AC翻折至△AB′C,连结B′D.
ABCD中,已知∠B=30°,将△ABC沿AC翻折至△AB′C,连结B′D.
(1)如图1,若![]() ,则∠ACB= °,BC= ;
,则∠ACB= °,BC= ;
(2)如图2,![]() ,BC=1,AB′与边CD相交于点E,求△AEC的面积;
,BC=1,AB′与边CD相交于点E,求△AEC的面积;
(3)已知![]() ,当BC长为多少时,是△AB′D直角三角形?
,当BC长为多少时,是△AB′D直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一扇门ABCD,宽度AB=1m,A到墙角E的距离AE=0.5m,设E,A,B在一条直线上,门打开后被与门所在墙面垂直的墙阻挡(EA⊥EB′),边BC靠在墙B'C'的位置.
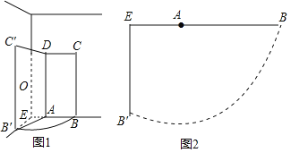
(1)求∠BAB'的度数;
(2)打开门后,门角上的点B在地面扫过的痕迹为弧BB',设弧BB'与两墙角线围成区域(如图2)的面积为S(m2),求S的值(π≈3.14,![]() ≈1.73,精确到0.1).
≈1.73,精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形OBCD中,OB=1,相邻两内角之比为1:2,将菱形OBCD绕顶点O顺时针旋转90°,得到菱形OB′C′D′视为一次旋转,则菱形旋转45次后点C的坐标为_____.
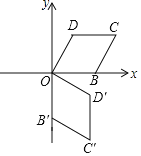
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30,且点P到AB边的距离为3,则四边形PMNQ的周长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某街道需要铺设管线的总长为9000![]() ,计划由甲队施工,每天完成150
,计划由甲队施工,每天完成150![]() .工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度
.工作一段时间后,因为天气原因,想要40天完工,所以增加了乙队.如图表示剩余管线的长度![]() 与甲队工作时间
与甲队工作时间![]() (天)之间的函数关系图象.
(天)之间的函数关系图象.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求线段![]() 所对应的函数解析式,并写出自变量
所对应的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)直接写出乙队工作25天后剩余管线的长度.
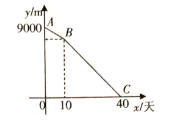
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com