练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，已知等腰梯形ABCD中，AD∥BC，AC⊥BD于O点，AC=5cm，求这个梯形的面积．

    答案：略
    解析：

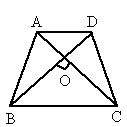
    解：过D点分别作DE∥AC，交BC延长线于E点，DF⊥BC于F点．

    因为梯形ABCD中，AD∥BC，

    所以四边形ACED是平行四边形(两组对边分别平行的四边形是平行四边形)，

    所以AC=DE，AD=CE(平行四边形对边相等)．

    因为AC⊥BD于O点，

    所以∠BOC=90°，

    所以∠BDE=90°(两直线平行，同位角相等)．

    因为AD=CD，

    所以AC=BD，

    所以△BDE是等腰直角三角形．

    因为AC=5cm，

    所以

    ．


    提示：

    要求梯形面积，需求AD与BC的和以及高，通过平移对角线可将AD＋BC转化到底边BC上，又知是等腰梯形且对角线互相垂直，所以梯形面积即为平移对角线后所得等腰直角三角形的面积．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    10、如图所示，已知等腰梯形ABCD的中位线EF的长为6，腰AD的长为5，则该等腰梯形的周长为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图所示，已知等腰梯形ABCD中，AD∥BC，AB=DC，AC与BD相交于点O．请在图中找出一对全等的三角形，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    23、如图所示，已知等腰梯形ABCD中，AD∥BC，AB=CD，点E为梯形外一点，且AE=DE．
    求证：BE=CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，已知等腰梯形ABCD中，AD∥BC，AB=CD，∠A=105°，则∠C等于（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网某村计划修建一条水渠，其横断面是等腰梯形，底角B为120°，如图所示，已知等腰梯形ABCD两腰与底边BC的和为4m，则梯形的最大面积为
     
    ．

    查看答案和解析>>

    同步练习册答案