
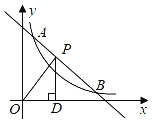
【题目】如图所示,一次函数y=﹣x+b与反比例函数y=![]() (x>0)的图象交于点A(1,3)和点B(3,m).
(x>0)的图象交于点A(1,3)和点B(3,m).
(1)填空:一次函数的表达式为 ,反比例函数的表达式为 ;
(2)点P是线段AB上一点,过点P作PD⊥x轴于点D,连接OP,若△POD的面积为S,求S的取值范围.
【答案】(1)y=﹣x+4,y=![]() ;(2)S的取值范围为
;(2)S的取值范围为![]() ≤S≤2.
≤S≤2.
【解析】
将点A的坐标分别代入一次函数y=﹣x+b与反比例函数y=![]() (x>0)得出B、K的值,再将b、k的值带入一次函数与反比例函数的表达式即可.
(x>0)得出B、K的值,再将b、k的值带入一次函数与反比例函数的表达式即可.
(2)将点B的坐标代入反比例函数表达式并解得:m=1,即点B(3,1),设点P(n,﹣n+4)(1≤n≤3),即S=![]() ×OD×PD,即-
×OD×PD,即-![]() <0且1≤n≤3,即可解答.
<0且1≤n≤3,即可解答.
(1)将点A的坐标分别代入一次函数y=﹣x+b与反比例函数y=![]() (x>0)并解得:b=4,k=3,
(x>0)并解得:b=4,k=3,
故一次函数与反比例函数的表达式分别为:y=﹣x+4,y=![]() ,
,
故答案为:y=﹣x+4,y=![]() ;
;
(2)将点B的坐标代入反比例函数表达式并解得:m=1,即点B(3,1),
设点P(n,﹣n+4)(1≤n≤3),
S=![]() ×OD×PD=
×OD×PD=![]() ×n×(﹣n+4)=﹣
×n×(﹣n+4)=﹣![]() (n﹣2)2+2,
(n﹣2)2+2,
∵-![]() <0且1≤n≤3,
<0且1≤n≤3,
∴当n=2时,S取得最大值为2;
当n=1或3时,S取得最小值为![]() ,
,
故S的取值范围为:![]() ≤S≤2.
≤S≤2.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x、y轴的正半轴上,顶点B的坐标为(4,2)点M是边BC上的一个动点(不与B、C重合),反比例函数![]() (k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
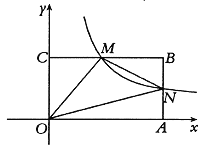
(1)当点M是边BC的中点时,求反比例函数的表达式;
(2)在点M的运动过程中,试证明:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
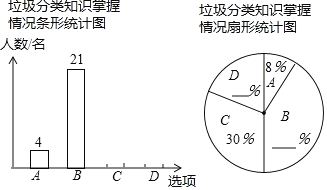
【题目】为响应市政府关于“垃圾不落地市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A:非常了解,B:比较了解,C:了解较少,D:不了解”四种,并将调查结果绘制成两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)若该校学生有2000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有 名;
(3)已知“非常了解”的同学有3名男生和1名女生,从中随机抽取2名进行垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
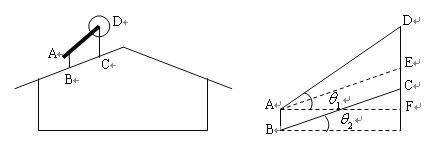
【题目】如图(9)所示(左图为实景侧视图,右图为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架![]() 和
和![]() (均与水平面垂直),再将集热板安装在
(均与水平面垂直),再将集热板安装在![]() 上.为使集热板吸热率更高,公司规定:
上.为使集热板吸热率更高,公司规定:![]() 与水平面夹角为
与水平面夹角为![]() ,且在水平线上的射影
,且在水平线上的射影![]() 为
为![]() .现已测量出屋顶斜面与水平面夹角为
.现已测量出屋顶斜面与水平面夹角为![]() ,并已知
,并已知![]() ,
,![]() .如果安装工人确定支架
.如果安装工人确定支架![]() 高为
高为![]() ,求支架
,求支架![]() 的高(结果精确到
的高(结果精确到![]() )?
)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某销售商准备在南充采购一批丝绸,经调查,用10000元采购A型丝绸的件数与用8000元采购B型丝绸的件数相等,一件A型丝绸进价比一件B型丝绸进价多100元.
(1)求一件A型、B型丝绸的进价分别为多少元?
(2)若销售商购进A型、B型丝绸共50件,其中A型的件数不大于B型的件数,且不少于16件,设购进A型丝绸m件.
①求m的取值范围.
②已知A型的售价是800元/件,销售成本为2n元/件;B型的售价为600元/件,销售成本为n元/件.如果50≤n≤150,求销售这批丝绸的最大利润w(元)与n(元)的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
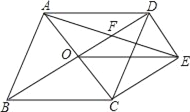
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
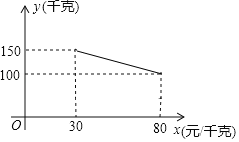
【题目】某超市销售一种商品,成本价为20元/千克,经市场调查,每天销售量y(千克)与销售单价x(元/千克)之间的关系如图所示,规定每千克售价不能低于30元,且不高于80元.
(1)求y与x之间的函数关系式;
(2)设每天的总利润为w元,当销售单价定为多少元时,该超市每天的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com