练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

     在，，–3.1416 ，π，，0．161161116……， 中无理数有       （    ）

    A．2个           B．3个         C．4个          D．5个

    C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

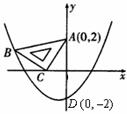
    如图：在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，与两坐标轴交点为点A和点C，与抛物线交于点B，其中点A（0，2），点B（– 3，1），抛物线与y轴交点D（0，– 2）．

    (1)  求抛物线的解析式；

    (2)  求点C的坐标；

    (3)  在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求所有点P的坐标；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图15.1，已知抛物线C经过原点，对称轴x=-3与抛物线相交于第三象限的点M，与x轴相交于点N，且tan∠MON = 3.

    (1)求抛物线C的解析式；

    (2)将抛物线C绕原点O旋转180º得到抛物线C’，抛物线C’与x轴的另一交点为A，B为抛物线C’上横向坐标为2的点.

    ①若P为线段AB上一动点，PD⊥y轴于点D，求△APD面积的最大值；

    ②过线段OA上的两点E、F分别作x轴的垂线，交折线 O –B -A于点E1、F1，再分别以线段EE1、FF1为边作如图15.2所示的等边△EE1E2、等边△FF1F2,点E以每秒1个单位长度的速度从点O向点A运动，点F以每秒1个单位长度的速度从点A向点O运动，当△EE1E2有一边与△FF1F2的某一边在同一直线上时，求时间t的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    王老师给同学们布置了这样一道习题：一个数的算术平方根为2m - 6，它的平方根为±（m - 2），求这个数。小张的解法如下：依题意可知，2m - 6是m - 2或者是-（m - 2）两数中的一个， （1）

    当2m - 6 = m - 2，解得m = 4。  （2）

    所以这个数为（2m - 6）=（2×4 - 6）= 4。  （3）

    当2m – 6 = -（m - 2）时，解得m =  。（4）

    所以这个数为（2m - 6）=（2×- 6）=  。 （5）

    综上可得，这个数为4或  。（6）

    王老师看后说，小张的解法是错误的。你知道小张错在哪里吗？为什么？请予改正。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

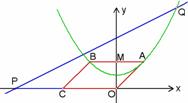
    如图1，在平面直角坐标系xOy中，抛物线的解析式是y ＝，点C的坐标为(–4，0)，平行四边形OABC的顶点A，B在抛物线上，AB与y轴交于点M，已知点Q(x，y)在抛物线上，点P(t，0)在x轴上． 

    (1) 写出点M的坐标；

    (2) 当四边形CMQP是以MQ，PC为腰的梯形时．

    ① 求t关于x的函数解析式和自变量x的取值范围；

    ② 当梯形CMQP的两底的长度之比为1∶2时，求t的值．

    查看答案和解析>>

    同步练习册答案