
(本题满分14分 ,第(1)小题5分,第(2)小题5分,第(3)小题4分)
如图,已知在等腰 Rt△ABC中,∠C=90°,斜边AB=2,若将△ABC翻折,折痕EF分别交边AC、边BC于点E和点F(点E不与A点重合,点F不与B点重合),且点C落在AB边上,记作点D.过点D作DK⊥AB,交射线AC于点K,设AD=x,y=cot∠CFE,



(1)求证:△DEK∽△DFB;
(2)求y关于x的函数解析式并写出定义域;
(3)联结CD,当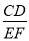 =
=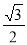 时,求x的值
时,求x的值
(1)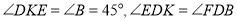 (2)
(2)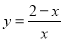 (
(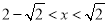 )
)
(3)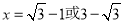
【解析】
试题分析:(1)根据互余的关系可证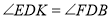 ,利用等腰直角三角形的性质可得
,利用等腰直角三角形的性质可得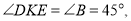 从而可证△DEK∽△DFB;(2)因为AD=x,所以DK=x,BD=2-x, 根据折叠可得Rt△DEF中,∠DFE=∠CFE,所以y=cot∠CFE= cot∠DFE=
从而可证△DEK∽△DFB;(2)因为AD=x,所以DK=x,BD=2-x, 根据折叠可得Rt△DEF中,∠DFE=∠CFE,所以y=cot∠CFE= cot∠DFE=  ,由△DEK∽△DFB可得
,由△DEK∽△DFB可得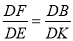 ,所以
,所以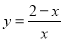 (
(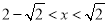 );(3)设CD交EF于点p,EF的中点为Q,连结CQ,根据题意可得
);(3)设CD交EF于点p,EF的中点为Q,连结CQ,根据题意可得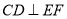 且PC=
且PC=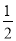 CD,
CD,
CQ=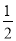 EF,根据
EF,根据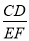 =
=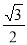 可得
可得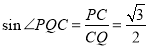 ,所以
,所以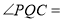 60°,从而∠CFE=∠DFE=30°,所以y=
60°,从而∠CFE=∠DFE=30°,所以y=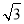 ,所以
,所以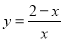 =
=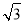 ,然后解方程即可.
,然后解方程即可.
试题解析:(1)根据题意可得∠EDK+∠KDF=90°,∠BDK+∠KDF=90°,所以 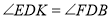 ,又因为△ABC是等腰直角三角形,所以
,又因为△ABC是等腰直角三角形,所以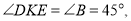 所以△DEK∽△DFB;(2)因为AD=x,所以DK=x,BD=2-x, 根据折叠可得Rt△DEF中,∠DFE=∠CFE,所以y=cot∠CFE= cot∠DFE=
所以△DEK∽△DFB;(2)因为AD=x,所以DK=x,BD=2-x, 根据折叠可得Rt△DEF中,∠DFE=∠CFE,所以y=cot∠CFE= cot∠DFE=  ,由△DEK∽△DFB可得
,由△DEK∽△DFB可得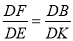 ,所以
,所以 (
( );(3)设CD交EF于点p,EF的中点为Q,连结CQ,由折叠可得
);(3)设CD交EF于点p,EF的中点为Q,连结CQ,由折叠可得 且PC=
且PC= CD,又△CEF是直角三角形,所以CQ=
CD,又△CEF是直角三角形,所以CQ=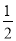 EF,又因为
EF,又因为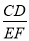 =
=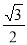 ,所以在Rt△PCQ中有
,所以在Rt△PCQ中有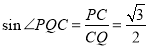 ,所以
,所以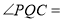 60°,所以∠CFE=∠FCQ=30°,所以∠CFE=∠DFE=30°,所以y=
60°,所以∠CFE=∠FCQ=30°,所以∠CFE=∠DFE=30°,所以y=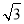 ,所以
,所以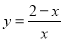 =
=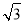 ,解得
,解得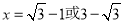 .
.
考点:1. 等腰直角三角形的性质;2.相似三角形的判定与性质;3. 直角三角形的性质;4.图形折叠的性质;5.特殊角的三角函数值;6.函数知识与几何知识的综合.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年山东潍坊高密四中文慧学校九年级上学期第一次月考数学试卷(解析版) 题型:填空题
平面直角坐标系中,A(—4,—2),B(0,—2),点C在x轴的正半轴,以O、B、C为顶点的三角形与△ABO相似,则点C的坐标是_________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年天津市九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,抛物线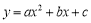
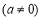 的对称轴为直线
的对称轴为直线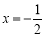 .下列结论中,正确的是( )
.下列结论中,正确的是( )
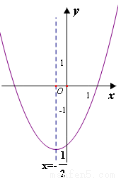
A.a<0
B.当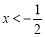 时, y随x的增大而增大
时, y随x的增大而增大
C.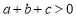
D.当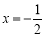 时,y的最小值是
时,y的最小值是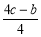
查看答案和解析>>
科目:初中数学 来源:2014-2015学年天津市九年级上学期期末考试数学试卷(解析版) 题型:选择题
为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元,设平均每次降价的百分率为x,则下面所列方程正确的是( )
A. 289(1-x)2=256
B. 256(1-x)2=289
C. 289(1-2x)=256
D. 256(1-2x)=289
查看答案和解析>>
科目:初中数学 来源:2014-2015学年上海市闸北九年级期末考试数学试卷(解析版) 题型:解答题
(本题满分10分, 第(1)小题6分,第(2)小题4分)
已知二次函数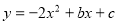 的图像经过点A(0,4)和B(1,-2).
的图像经过点A(0,4)和B(1,-2).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为y=a(x+m)2+k的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省七校九年级上学期联考数学试卷(解析版) 题型:解答题
((8分))如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
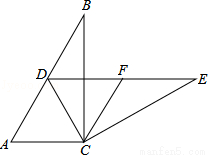
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年内蒙古巴彦淖尔乌拉特前旗四中九年级上学期期末考试数学试卷(解析版) 题型:选择题
某种衬衣原价168元,连续两次降价a%后售价为128元.下面所列方程中正确的是( )
A.168(1+a%) 2=128 B.168(1-a%)2=128
C.168(1-2a%)=128 D.168(1-a2%)=128
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com