练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．已知下列命题：①相等的角是对顶角；②互补的角一定是邻补角；③互补的两个角一定是一个锐角，另一个为钝角；④平行于同一条直线的两直线平行；⑤邻补角的平分线互相垂直．其中，正确命题的个数为（　　）
    A．0B．1个C．2个D．3个

    分析 分别利用对顶角以及邻补角的定义结合角平分线的性质、平行线的性质分别分析得出答案．

    解答 解：①相等的角是对顶角，错误；
    ②互补的角一定是邻补角，错误；
    ③互补的两个角一定是一个锐角，另一个为钝角，可以为两个直角；
    ④平行于同一条直线的两直线平行，正确；
    ⑤邻补角的平分线互相垂直，正确；
    故选；C．

    点评 此题主要考查了命题与定理，正确把握相关性质是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    18．按如图的运算程序，能使输出结果为3的x，y的值是（　　）
    A．x=5，y=-2B．x=3，y=-3C．x=-4，y=2D．x=-3，y=-9

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

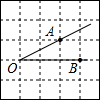    19．如图，在边长为1的小正方形组成的网格中，点A、B、O为格点，则tan∠AOB=（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{3}$C．$\frac{\sqrt{10}}{5}$D．$\frac{\sqrt{5}}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．二次函数y=x2+（2m+1）x+m2的图象交x轴于A（x1，0）、B（x2，0），已知x1＜x2且x12+x1•x2+x22=21．
    （1）求m的值；
    （2）设直线AM交抛物线于点M，若∠MAB为锐角，且△ABM的面积为6，求直线AM的解析式；
    （3）对于（2）中的点M，若AP⊥AM交抛物线于另一点P，问在x轴上是否存在一点Q，使得以A、P、Q为顶点的三角形与△ABM相似？如果存在，求出点Q的坐标；如果不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于点A（-4，0），B（1，0），与y轴交于点D（0，4），点C（-2，n）也在此抛物线上．
    （1）求此抛物线的解析式及点C的坐标；
    （2）设BC交y轴于点E，连接AE，AC请判断△ACE的形状，并说明理由；
    （3）连接AD交BC于点F，试问：以A，B，F为顶点的三角形与△ABC相似吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．对每个x，y是y1=2x，y2=x+2，y3=-$\frac{3}{2}$x+12三个值中的最小值，则当x变化时，函数y的最大值是6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，抛物线y=-x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点A的坐标为（-1，0），与y轴交于点C（0，3），作直线BC．动点P在x轴上运动，过点P作PM⊥x轴，交抛物线于点M，交直线BC于点N，设点P的横坐标为m．
    （1）求抛物线的解析式和直线BC的解析式；
    （2）当点P在线段OB上运动时，求线段MN的最大值；
    （3）当点P在线段OB上运动时，若△CMN是以MN为腰的等腰直角三角形时，求m的值；
    （4）当以C、O、M、N为顶点的四边形是平行四边形时，直接写出m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．小强是校学生会体育部部长，他想了解现在同学们更喜欢什么球类运动，以便学生会组织受欢迎的比赛．于是他设计了调查问卷，在全校每个班都随机选取了一定数量的学生进行调查，调查问卷如图：
    调查问卷
    你最喜欢的球类运动是（A　）（单选）
    A．篮球 B．足球 C．排球 D．乒乓球 E．羽毛球 F．其他
    小强根据统计数据制作的各活动小组人数分布情况的统计表和扇形统计图如图：
    组别篮球足球排球乒乓球羽毛球其他
    人数69m27n969
    （1）请你写出统计表的空缺部分的人数m=63，n=36；
    （2）在扇形统计图中，羽毛球所对应扇形的圆心角等于115.2°；
    （3）请你根据调查结果，给小强部长简要提出合理化的建议．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，阴影部分是两个正方形，其他三个图形是一个正方形和两个直角三角形，则阴影部分的面积和为81．

    查看答案和解析>>

    同步练习册答案