
分析 首先计算乘方、乘法,然后从左向右依次计算,求出算式的值是多少即可.
解答 解:(-1)2017+2•cos60°-${(-\frac{1}{2})}^{-2}$+${(\sqrt{3}-\sqrt{2})}^{0}$
=-1+2×$\frac{1}{2}$-4+1
=-1+1-3
=-3
点评 此题主要考查了实数的运算,零指数幂、负整数指数幂的运算方法以及特殊角的三角函数值的求法,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.


科目:初中数学 来源: 题型:填空题
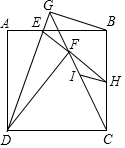 如图,E为正方形ABCD边AB上的一点,且AD=3,AE=1,将△ADE沿DE翻折得到△FDE,连接并延长CF与DE延长线相交于点G,连接BG,延长EF交BC于H,过点H作HI∥BG,则HI的长为$\frac{3}{10}$$\sqrt{10}$.
如图,E为正方形ABCD边AB上的一点,且AD=3,AE=1,将△ADE沿DE翻折得到△FDE,连接并延长CF与DE延长线相交于点G,连接BG,延长EF交BC于H,过点H作HI∥BG,则HI的长为$\frac{3}{10}$$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则AD的长为( )
如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则AD的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
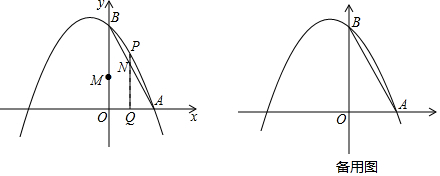
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com