
【题目】已知:AB,PQ是圆O的两条直径,连接PB,AQ.
(1)如图①,求证:AQ∥BP,AG∥BP; 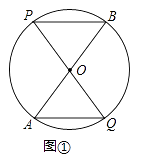
(2)如图②,过点B作BC⊥PQ于点D,交圆O于点C,在DG上取一点K,使DK=DP,求证:四边形AQKC是平行四边形. 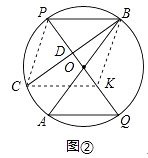
【答案】
(1)证明:∵ ![]() =
= ![]() ,
,
∴∠P=∠A,
∵OA=OQ,
∴∠A=∠Q,
∴∠P=∠Q,
∴AQ∥PB.
∵∠AOQ=∠BOP,
∴ ![]() =
= ![]() ,
,
∴AQ=BP;
(2)证明:∵PQ⊥BC,
∴BD=CD,
又∵PD=DK,
∴BC与PK互相垂直且平分,
∴四边形BKCP为菱形;
∴PB∥CK,且PB=CK,
∵PB∥AQ,
∴CK∥AQ,
∵PB=AQ,
∴CK=AQ,
∵CK∥AQ,且CK=AQ,
∴四边形AQKC为平行四边形.
【解析】(1)由同弧所对的圆周角相等得出∠P=∠A,由OA=OQ得出∠A=∠Q,那么∠P=∠Q,AQ∥PB.根据∠AOQ=∠BOP,得到 ![]() =
= ![]() ,那么AQ=BP;(2)先由垂径定理得出BD=CD,又PD=DK,得出四边形BKCP为菱形,根据菱形的性质得出PB∥CK,再证明CK∥AQ,且CK=AQ,那么四边形AQKC为平行四边形.
,那么AQ=BP;(2)先由垂径定理得出BD=CD,又PD=DK,得出四边形BKCP为菱形,根据菱形的性质得出PB∥CK,再证明CK∥AQ,且CK=AQ,那么四边形AQKC为平行四边形.
【考点精析】本题主要考查了平行四边形的判定和圆周角定理的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
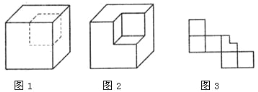
【题目】如图![]() ,大正方体上截去一个小正方体后,可得到图
,大正方体上截去一个小正方体后,可得到图![]() 的几何体.
的几何体.
![]() 设原大正方体的表面积为
设原大正方体的表面积为![]() ,图
,图![]() 中几何体的表面积为
中几何体的表面积为![]() ,那么
,那么![]() 与
与![]() 的大小关系是( )
的大小关系是( )
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、不确定
、不确定
![]() 小明说:“设图
小明说:“设图![]() 中大正方体各棱的长度之和为
中大正方体各棱的长度之和为![]() ,图
,图![]() 中几何体各棱的长度之和为
中几何体各棱的长度之和为![]() ,那么
,那么![]() 比
比![]() 正好多出大正方体
正好多出大正方体![]() 条棱的长度.”若设大正方体的棱长为
条棱的长度.”若设大正方体的棱长为![]() ,小正方体的棱长为
,小正方体的棱长为![]() ,请问
,请问![]() 为何值时,小明的说法才正确?
为何值时,小明的说法才正确?
![]() 如果截去的小正方体的棱长为大正方体棱长的一半,那么图
如果截去的小正方体的棱长为大正方体棱长的一半,那么图![]() 是图
是图![]() 中几何体的表面展开图吗?如有错误,请在图
中几何体的表面展开图吗?如有错误,请在图![]() 中修正.
中修正.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有75名工人生产A、B两种零件,一名工人每天可生产A种零件15个或B 种 零件20个,已知1个B种零件需要配3个A种零件,该车间应如何分配工人,才能保证每天生产的两种零件恰好配套?设应安排x名工人生产A种零件,根据题意,列出的方程是___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC和Rt△DBE中,∠ABC=∠EBD=90°,AB=BC,DB=EB.显然可得结论AD=EC,AD⊥EC.
(1)阅读:当Rt△DBE绕点B逆时针旋转到图2的位置时,连接AD,CE.求证:AD=EC,AD⊥EC.
下面给出了小亮的证明过程,请你把小亮的证明过程填写完整:
∵∠ABC=∠EBD,∴∠ABC-∠ABE=∠EBD-∠ABE,即∠EBC=∠DBA.在△EBC和△DBA中,
BC=BA,∠______=∠______,BE=BD,
∴△EBC≌△DBA,∴CE=AD,∠ECB=∠______.
∵∠ECB+∠ACE+∠CAB=90°,∴∠DAB+∠ACE+∠CAB=90°,∴∠______=90°,∴AD⊥EC.
(2)类比:当Rt△DBE绕点B逆时针旋转90°得到图3时,连接AD,CE.问(1)中线段AD,EC间的数量关系和位置关系还成立吗?若成立,请给出证明;若不成立,请说明理由;
(3)拓展:当Rt△DBE绕点B逆时针旋转到图4时,连接AD,CE.请说明AD,EC间的数量关系和位置关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)23﹣6×(﹣3)+2×(﹣4) ; (2)﹣16﹣(﹣5)+23﹣|﹣![]() |
|
(3)﹣(1﹣0.5)÷![]() ×[2+(﹣4)2].
×[2+(﹣4)2].
(4)(4)﹣22﹣(﹣![]() )2×
)2×![]() +6÷|
+6÷|![]() ﹣2|+(﹣1)5×(﹣
﹣2|+(﹣1)5×(﹣![]() )2.
)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两站相距240千米,从甲站开出一列慢车,速度为每小时80千米,从乙站开出一列快车,速度为每小时120千米.
(1)若两车同时开出,背向而行,则经过多长时间两车相距540千米?
(2)若两车同时开出,同向而行(快车在后),则经过多长时间快车可追上慢车?
(3)若两车同时开出,同向而行(慢车在后),则经过多长时间两车相距300千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com