
【题目】定义:如果一个y与x的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如:y=![]() +1的图象向左平移2个单位,再向下平移1个单位得到y=
+1的图象向左平移2个单位,再向下平移1个单位得到y=![]() 的图象,则y=
的图象,则y=![]() +1是y与x的“反比例平移函数”.
+1是y与x的“反比例平移函数”.
(1)若(x+3)(y+2)=8,求y与x的函数表达式,并判断这个函数是否为“反比例平移函数”?
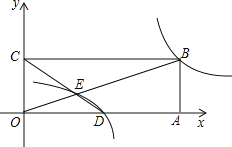
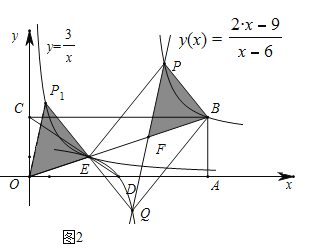
(2)如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3),点D是OA的中点,连接OB、CD交于点E,“反比例平移函数”y=![]() 的图象经过B、E两点,则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
的图象经过B、E两点,则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
(3)在(2)的条件下,已知过线段BE中点的一条直线l交这个“反比例平移函数”图象于P、Q两点(P在Q的右侧),若B、E、P、Q为顶点组成的四边形面积为16,请求出点P的坐标.
【答案】(1)y=![]() ﹣2,是“反比例平移函数”;(2)y=2+
﹣2,是“反比例平移函数”;(2)y=2+![]() ,y=
,y=![]() ;(3)点P的坐标为:(7,5)或(15,
;(3)点P的坐标为:(7,5)或(15,![]() ).
).
【解析】
(1)将已知式变形用x表示y,再由“反比例平移函数”的定义即可判断;
(2)故点E(3,1),将B、E的坐标代入y=![]() ,即可求解;
,即可求解;
(3)由(2)可知![]() 是
是![]() 的“反比例平移函数”,而且E点与B点是两函数的对应点,线段BE的中点F为由反比例函数
的“反比例平移函数”,而且E点与B点是两函数的对应点,线段BE的中点F为由反比例函数![]() 对称中心,得四边形PEQB为平行四边形.四边形PEQB的面积为16,S△PFB=4,利用平移对应关系先在
对称中心,得四边形PEQB为平行四边形.四边形PEQB的面积为16,S△PFB=4,利用平移对应关系先在![]() 求P1(P的对应点),即可求出P点坐标.
求P1(P的对应点),即可求出P点坐标.
解:(1)![]() ,则
,则![]() ,
,
该函数图象向右平移3个单位,再向上平移2个单位得到![]() 的图象,
的图象,
故:函数是“反比例平移函数”;
(2)点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,则点
,点D是OA的中点,则点![]() ,
,
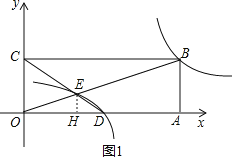
∴直线OB的解析式为:![]() ,直线CD的解析式为:
,直线CD的解析式为:![]() ,
,
联立的方程组: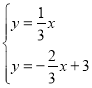 ,
,
解得![]() , 故点
, 故点![]() ,
,
将B、E的坐标代入![]() 得:
得: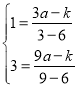 ,解得:
,解得:![]() ,
,
故这个“反比例平移函数”的表达式为![]() ,
,
故变换后的反比例函数表达式为![]() ,
,
故答案为:![]() ,
,![]() ;
;
(3)∵![]() ,
,![]() ,线段BE的中点为F,
,线段BE的中点为F,
∴![]() ,
,
由(2)可知:![]() 是
是![]() 的“反比例平移函数”,由
的“反比例平移函数”,由![]() 向下左6个单位,向下2个单位可得
向下左6个单位,向下2个单位可得![]() ,
,
∴点B与点E、点F与点O是平移的对应点,
所以![]() 存在点
存在点![]() 与所求点P对应,
与所求点P对应,
如图,由反比例函数中心对称性,四边形PEQB为平行四边形.
![]() 四边形PEQB的面积为16,
四边形PEQB的面积为16,![]() ,
,
![]() ,
,
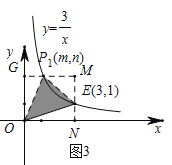
I.当点P在点B左侧时,设其对应点坐标为设![]() ,则
,则![]() 在E点左侧,如图:简化构造矩形求面积得,
在E点左侧,如图:简化构造矩形求面积得,
![]() .
.
![]() ,解得:
,解得:![]() ,而
,而![]() ,
,
故![]() ,
,![]() ,故:
,故:![]() ,
,
![]() 点P的坐标为
点P的坐标为![]() .
.
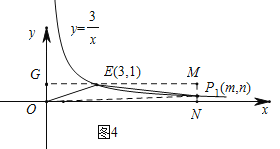
![]() .当点P在点B右侧时,对应如图,同理可得点P的坐标为
.当点P在点B右侧时,对应如图,同理可得点P的坐标为![]() ,
,
综上,点P的坐标为:![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点P、点Q同时从点B出发,点P以
,点P、点Q同时从点B出发,点P以![]() 的速度沿
的速度沿![]() 运动,终点为C,点Q以
运动,终点为C,点Q以![]() 的速度沿
的速度沿![]() 运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,
运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,![]() 的面积为
的面积为![]() ,已知y与t的函数关系的图象如图
,已知y与t的函数关系的图象如图![]() 曲线OM和MN均为抛物线的一部分
曲线OM和MN均为抛物线的一部分![]() ,给出以下结论:
,给出以下结论:![]() ;
;![]() 曲线MN的解析式为
曲线MN的解析式为![]() ;
;![]() 线段PQ的长度的最大值为
线段PQ的长度的最大值为![]() ;
;![]() 若
若![]() 与
与![]() 相似,则
相似,则![]() 秒
秒![]() 其中正确的是
其中正确的是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的点,
上的点,![]() 是线段
是线段![]() 上的点,且
上的点,且![]() .
.
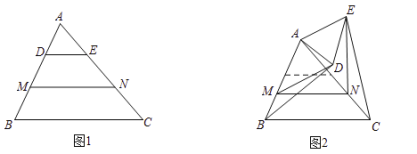
(1)观察猜想
如图1,若点![]() 是线段
是线段![]() 的三等分点,则
的三等分点,则![]() __________,
__________,![]() ___________.由此,我们猜想线段
___________.由此,我们猜想线段![]() ,
,![]() ,
,![]() ,
,![]() 之间满足的数量关系是_________.
之间满足的数量关系是_________.
(2)类比探究
将![]() 在平面内绕点
在平面内绕点![]() 按逆时针方向旋转一定的角度,连接
按逆时针方向旋转一定的角度,连接![]() ,
,![]() ,
,![]() ,
,![]() ,猜想在旋转的过程中,(1)中的结论是否仍然成立?若成立,请仅就图2的情形给出证明;若不成立,请说明理由.
,猜想在旋转的过程中,(1)中的结论是否仍然成立?若成立,请仅就图2的情形给出证明;若不成立,请说明理由.
(3)解决问题
将![]() 在平面内绕点
在平面内绕点![]() 自由旋转,若
自由旋转,若![]() ,请直接写出线段
,请直接写出线段![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
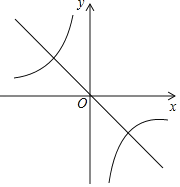
【题目】反比函数![]() 的图象如图所示.
的图象如图所示.
(1)求m的值;
(2)当x>﹣1时,y的取值范围是 ;
(3)当直线y2=﹣x与双曲线![]() 交于A、B两点(A在B的左边)时,结合图象,求出在什么范围时y2>y1?
交于A、B两点(A在B的左边)时,结合图象,求出在什么范围时y2>y1?
查看答案和解析>>
科目:初中数学 来源: 题型:
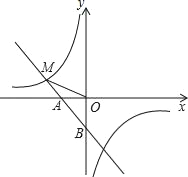
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)当y2>y1时,求x的取值范围;
(3)求点B到直线OM的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 三地顺次在同-直线上,甲、乙两人均骑车从
三地顺次在同-直线上,甲、乙两人均骑车从![]() 地出发,向
地出发,向![]() 地匀速行驶.甲比乙早出发
地匀速行驶.甲比乙早出发![]() 分钟;甲到达
分钟;甲到达![]() 地并休息了
地并休息了![]() 分钟后,乙追上了甲.甲、乙同时从
分钟后,乙追上了甲.甲、乙同时从![]() 地以各自原速继续向
地以各自原速继续向![]() 地行驶.当乙到达
地行驶.当乙到达![]() 地后,乙立即掉头并提速为原速的
地后,乙立即掉头并提速为原速的![]() 倍按原路返回
倍按原路返回![]() 地,而甲也立即提速为原速的二倍继续向
地,而甲也立即提速为原速的二倍继续向![]() 地行驶,到达
地行驶,到达![]() 地就停止.若甲、乙间的距离
地就停止.若甲、乙间的距离![]() (米)与甲出发的时间
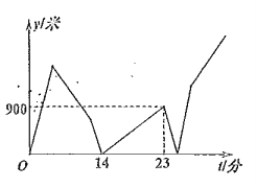
(米)与甲出发的时间![]() (分)之间的函数关系如图所示,则下列说法错误的是( )
(分)之间的函数关系如图所示,则下列说法错误的是( )
A.甲、乙提速前的速度分别为![]() 米/分、
米/分、![]() 米/分.
米/分.
B.![]() 两地相距
两地相距![]() 米
米
C.甲从![]() 地到
地到![]() 地共用时
地共用时![]() 分钟
分钟
D.当甲到达![]() 地时,乙距
地时,乙距![]() 地
地![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】涌泉镇是中国无核蜜桔之乡,已知某蜜桔种植大户冯大爷的蜜桔成本为2元/千克,如果在未来90天蜜桔的销售单价p(元/千克)与时间t(天)之间的函数关系式为p=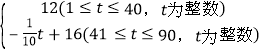 ,且蜜桔的日销量y(千克)与时间t(天)满足一次函数关系,其部分数据如下表所示:
,且蜜桔的日销量y(千克)与时间t(天)满足一次函数关系,其部分数据如下表所示:
时间t/天 | 1 | 10 | 20 | 40 | 70 | 90 |
日销售量y/千克 | 105 | 150 | 200 | 300 | 450 | 550 |
(1)求y与t之间的函数表达式;
(2)在未来90天的销售中,预测哪一天的日销售利润最大?最大日销售利润为多少元?
(3)在实际销售的后50天中,冯大爷决定每销售1千克蜜桔就捐赠n元利润(n<5)给留守儿童作为助学金,销售过程中冯大爷发现,恰好从第51天开始,和前一天相比,扣除捐赠后的日销售利润逐日减少,请求出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(a﹣1)x2+3ax+1图象上的四个点的坐标为(x1,m),(x2,m),(x3,n),(x4,n),其中m<n.下列结论可能正确的是( )
A.若a>![]() ,则 x1<x2<x3<x4
,则 x1<x2<x3<x4
B.若a>![]() ,则 x4<x1<x2<x3
,则 x4<x1<x2<x3
C.若a<﹣![]() ,则 x1<x3<x2<x4
,则 x1<x3<x2<x4
D.若a<﹣![]() ,则 x3<x2<x1<x4
,则 x3<x2<x1<x4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com