
分析 (1)将特殊角的三角函数值代入后进行化简求值即可;
(2)将特殊角的三角函数值代入,然后化简二次根式,最后合并同类项即可.
解答 解:(1)原式=$\frac{(\frac{\sqrt{3}}{2})^{2}+(\frac{1}{2})^{2}}{\sqrt{3}×\frac{\sqrt{3}}{2}}$+$\sqrt{3}$=$\frac{2}{3}$+$\sqrt{3}$;
(2)原式=2×$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$-2×$\frac{1}{2}$×1+$\sqrt{6}$×$\sqrt{3}$=1-1+3$\sqrt{2}$=3$\sqrt{2}$.
点评 本题考查了特殊角的三角函数值.应用中要熟记特殊角的三角函数值,一是按值的变化规律去记,正弦逐渐增大,余弦逐渐减小,正切逐渐增大;二是按特殊直角三角形中各边特殊值规律去记.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
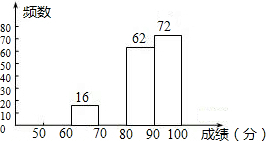 某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了m名学生的得分进行统计
某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了m名学生的得分进行统计| 成绩x(分) | 频数 | 频率 |
| 50≤x<60 | 10 | a |
| 60≤x<70 | 16 | 0.08 |
| 70≤x<80 | b | 0.02 |
| 80≤x<90 | 62 | c |
| 90≤x<100 | 72 | 0.36 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{98}$ | C. | $\sqrt{50}$ | D. | $\sqrt{48}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com