4
分析:根据ABCD是矩形,BD是对角线,设BC′与AD的交点为P,则可判断△ABD≌△CBD,△BDC′≌△BDC,△BDC′≌△DBA,△APB≌△C′PD共四对.并分别进行证明.
解答:
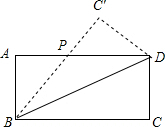
解:如图,设BC′与AD的交点为P
①△ABD≌△CBD
∵ABCD是矩形
∴AB=DC,AD=BC,BD=BD
∴△ABD≌△CBD;
②△BDC′≌△BDC
∵BC=BC′,∠CBD=∠C′BD,BD=BD
∴△BDC′≌△BDC;
③△BDC′≌△DBA
∵△ABD≌△CBD,△BDC′≌△BDC
∴△BDC′≌△DBA;
④△APB≌△C′PD
∵AB=C′D,∠A=∠C′,∠APB=∠C′PD
∴△APB≌△C′PD.
∴图中(包括虚,实线)共有4对全等三角形.
故填4.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理.

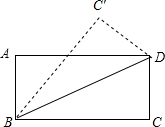 如图中的△BDC′是将矩形纸片ABCD沿对角线BD折叠到的.则图中(包括虚,实线)共有________对全等三角形.
如图中的△BDC′是将矩形纸片ABCD沿对角线BD折叠到的.则图中(包括虚,实线)共有________对全等三角形. 解:如图,设BC′与AD的交点为P
解:如图,设BC′与AD的交点为P
