
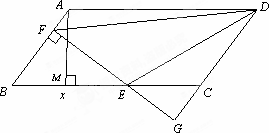
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,连结DE,DF.
(1)求证:ΔBEF∽ΔCEG.
(2)当点E在线段BC上运动时,△BEF和△CEG的周长之间有什么关系?并说明你的理由.
(3)设BE=x,△DEF的面积为y,请你求出y和x之间的函数关系式,并求出当x为何值时,y有最大值,最大值是多少?
|
(1)因为四边形ABCD是平行四边形,所以 所以 所以 (2) 理由一: 过点C作FG的平行线交直线AB于H,
因为GF⊥AB,所以四边形FHCG为矩形.所以FH=CG,FG=CH 因此, 由BC=10,AB=5,AM=4,可得CH=8,BH=6, 所以BC+CH+BH=24 6分 理由二: 由AB=5,AM=4,可知 在Rt△BEF与Rt△GCE中,有: 所以,△BEF的周长是 又BE+CE=10,因此 (3)设BE=x,则 所以 配方得: 所以,当 最大值为 |


科目:初中数学 来源: 题型:
 次方程x2-7x+12=0的两个根,且OA>OB.
次方程x2-7x+12=0的两个根,且OA>OB.| OA |
| AB |
| 16 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com